Espaciotiempo y las geodésicas

Clase 7

Plan de la Clase

• La métrica del espacio-tiempo.
• Ejemplo: la métrica de Minkowski.
• La ecuación geodésica.

La métrica

• En cualquier sistema de coordenadas, el elemento de línea es:

$$\boxed{ ds^2 = g_{ij} dx^i dx^j }$$

• Dicho de otra forma, $ds^2$ es independiente de las coordenadas (es una cantidad escalar).
• El espacio puede ser plano o curvo dependiendo de cómo se comporta $g_{ij}$.
  • La curvatura se relaciona a sus segundas derivadas.

Espacio vs espaciotiempo

• Hasta ahora, hemos descrito espacios puramente espaciales.
  • Dado que el tiempo no es absoluto en RG, para describir eventos necesitamos agregar una coordenada temporal $t$:

$$x^\mu = (t, x, y, z)$$

• En general, otro observador podrá identificar el mismo evento con coordenadas $x'^\mu = (t', x', y', z')$.
  • Ambos se podrán relacionar de forma unívoca mediante una transformación de coordenadas $x^\mu\to x'^\mu$.

Espacio vs espaciotiempo

• Notar que las métricas anteriores (espaciales) siempre fueron tales que las distancias medidas son positivas .
  • Al agregar una coordenada temporal, esto último ya no será cierto.
• Por convención, $g_{00}$ será negativa.
• Entonces, $ds^2$ podrá ser positivo, negativo, o cero.

El Espaciotiempo de Minkowski

• Un caso particular es el espaciotiempo plano, que describe la Relatividad Especial, y se denomina la métrica de Minkowski:

$$g_{\mu\nu} = \eta_{\mu\nu} = \begin{bmatrix} -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

• En coordenadas cartesianas $x^\mu = (t, x, y, z)$, tenemos:

$$ds^2 = -dt^2 + dx^2 + dy^2 + dz^2$$

Curvatura y Geodésicas

• En Relatividad General, la gravedad no es una fuerza.
• Los objetos siguen las trayectorias más rectas posibles en un espacio-tiempo curvo.
  • Estas trayectorias se llaman geodésicas.

En el ejemplo anterior de una esfera:

• En la Tierra, la ruta más corta entre dos puntos es un arco de un círculo máximo.

Curvatura y Geodésicas

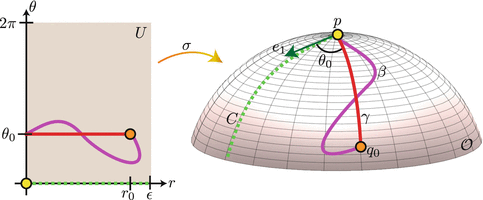
Derivadas de tensores

• La noción de derivada está bien definida para escalares.
  • Simplemente comparamos su valor en dos puntos distintos.
  • Por ejemplo:

$$\partial_x f(t,x,y,z) = \lim_{\Delta x\to0} \frac{f(t,x+\Delta x,y,z) - f(t,x,y,z)}{\Delta x}$$

Derivadas de tensores

• En el caso de tensores de rango 1 o más (vectores, tensores), esto genera una ambiguedad:
  • Si queremos comparar dos vectores, debemos "mover" (transportar) uno de ellos hasta que "las flechas coincidan en su origen".
  • Sin embargo, en este proceso puede estar "contaminado artificialmente" ya que las componentes del vector pueden cambiar por el hecho de que vectores base cambian.

La derivada covariante

• En espacios curvos, la noción de derivada tradicional (parcial) se generaliza a la derivada covariante:

$$\nabla_\mu v^\alpha = \partial_\mu v^\alpha + \Gamma^\alpha_{\mu\nu} v^\nu$$

$$\nabla_\mu v_\alpha = \partial_\mu v_\alpha - \Gamma^\nu_{\mu\alpha} v_\nu$$

• Esta derivada permite comparar vectores tras descontar el cambio en los vectores bases, i.e. es la diferencia "real".

La derivada covariante

• Para tensores de rango 2:

$$\nabla_\lambda T^{\mu\nu} = \partial_\lambda T^{\mu\nu} + \Gamma^\mu_{\lambda\rho} T^{\rho\nu} + \Gamma^\nu_{\lambda\rho} T^{\mu\rho}$$

$$\nabla_\lambda T_{\mu\nu} = \partial_\lambda T_{\mu\nu} - \Gamma^\rho_{\lambda\mu} T_{\rho\nu} - \Gamma^\rho_{\lambda\nu} T_{\mu\rho}$$

$$\nabla_\lambda T_{\mu\nu} = \partial_\lambda T_{\mu\nu} - \Gamma^\rho_{\lambda\mu} T_{\rho\nu} - \Gamma^\rho_{\lambda\nu} T_{\mu\rho}$$

• Es decir, aplicamos un objeto "$\Gamma$" por cada índice.
• Para escalares (rango 0), esta se reduce a la derivada parcial.

La conexión: símbolos de Christoffel

• En la definición anterior, aparece un objeto llamado "conexión":

$$\Gamma^\alpha_{\mu\nu} = \frac{1}{2} g^{\alpha\beta} \left(\partial_\mu g_{\nu\beta} + \partial_\nu g_{\mu\beta} - \partial_\beta g_{\mu\nu}\right)$$

• La conexión precisamente mide cómo cambia la base de vectores al desplazarse por la variedad
• Satisface la condición de compatibilidad con la métrica:

$$\nabla_\alpha g_{\mu\nu} = 0.$$

Geodésicas

• En Física Newtoniana, para un objeto libre de fuerzas externas:

$$a^i=\frac{dv^i}{dt}=\frac{d^2x^i}{dt^2} = 0$$

por lo tanto se mueve en una trayectoria rectilínea con velocidad constante (tanto magnitud como dirección).

Geodésicas

• En Relatividad, definimos la cuadri-velocidad de un objeto respecto a un observador como

$$v^\mu=\frac{dx^\mu}{d\tau}$$

donde $\tau$ es su tiempo propio (medido por un reloj del observador).

La ecuación geodésica

• En RG, la gravedad ya no es una fuerza, i.e. las partículas son "libres" (a menos que incluyamos una fuerza real).
• Luego, podemos generalizar el concepto de "recta" a un espaciotiempo curvo en función de la cuadri-aceleración como:

$$a^\mu=\frac{Dv^\mu}{D\tau}=u^\mu \nabla_\nu u^\nu = 0$$

• Esta se denomina ecuación geodésica.

La ecuación geodésica

• Explícitamente, la ecuación geodésica toma la forma:

$$\boxed{ \frac{d^2 x^\alpha}{d\tau^2} + \Gamma^\alpha_{\mu\nu} \frac{dx^\mu}{d\tau}\frac{dx^\nu}{d\tau} = 0 }$$

• Formalmente, las geodésicas son trayectorias que extremizan la acción que describe una partícula en la RG.
  • Los cuerpos con masa siguen trayectorias que maximizan el tiempo propio.