La Gravedad Newtoniana pt 2

Clase 3

Plan de la Clase

  • La ecuación de Poisson para el potencial gravitacional y algunas soluciones.
  • Gravedad vs aceleración.

Ejemplo: Resolver la ecuación de Poisson para una masa puntual

Resuelva la ecuación de Poisson

∇2Φ=4πGρ\nabla^2 \Phi = 4\pi G \rho

para encontrar el campo producido por una masa puntual.

Ejemplo: Resolver la ecuación de Poisson para una masa puntual

Desarrollado en clase anterior, hasta aplicación de la Ley de Gauss

Ejemplo: Resolver la ecuación de Poisson para una masa puntual

Ahora aplicamos las condiciones de borde sobre la solución.

  1. Físicamente, esperamos una solución asintóticamente plana:

    Φ(r→∞)→0  ⟹  C2=0\Phi(r\to\infty)\to0 \implies C_2=0

  2. Para determinar C1C_1, podemos aplicar la Ley de Gauss:

∮Sg⋅dS=−∮S∇Φ⋅dS=−4πGMenc\oint_S \mathbf{g} \cdot dS =-\oint_S \mathbf{\nabla}\Phi \cdot dS = -4\pi G M_{\text{enc}}

Ejemplo: Resolver la ecuación de Poisson para una masa puntual

Integrando sobre una esfera de radio ϵ\epsilon, con dS=r2dΩdS = r^2 d\Omega, encontramos que:

dΦdr∣r=ϵ4πr2=4πGM\left. \frac{d\Phi}{dr} \right|_{r=\epsilon} 4\pi r^2 = 4\pi G M

Por lo que C1=GMC_1 = G M. La solución final es entonces la esperada:

Φ(r)=−GMr.\Phi(r) = -\frac{GM}{r}.

Comentario sobre la solución

  • Notar que aplicando la Ley de Gauss desde un comienzo también habría sido posible encontrar la solución.
    • Sin embargo, no la usamos ya que el ejercicio nos pedía resolver la ecuación de Poisson.
  • En general utilizar la Ley de Gauss requiere menos cálculo.
    • Tiene alguna desvetaja este método de solución?

Ejemplo: Potencial Gravitacional de una Esfera Uniforme

Considere una esfera uniforme de radio RR y densidad ρ\rho constante.
Resolver la ecuación de Poisson ∇2Φ=4πGρ\nabla^2 \Phi = 4 \pi G \rho y encontrar el potencial asociado a dicha esfera.

Ejemplo: Potencial Gravitacional de una Esfera Uniforme

  • En coordenadas esféricas, la solución es una función radial.
  • Solución interior (r<Rr<R):

Φ(r)=−2πGρ3r2+C\Phi(r) = -\frac{2\pi G \rho}{3} r^2 + C

  • Solución exterior (r>Rr>R):

Φ(r)=−GMr\Phi(r) = -G \frac{M}{r}

Ejemplo: Potencial Gravitacional de una Esfera Uniforme

  • ¿Cómo fijar la constante de integración CC?

Gravedad vs Aceleración

  • Galileo Galilei (~1590) estudió la gravedad lanzando objetos desde la torre de Pisa y observando su movimiento.

    • Concluyó que todos los cuerpos caen con la misma aceleración, independiente de cual sea su masa.

  • Einstein propuso el "experimento mental" de un ascensor para analizar esto en mayor detalle.

Experimento del ascensor

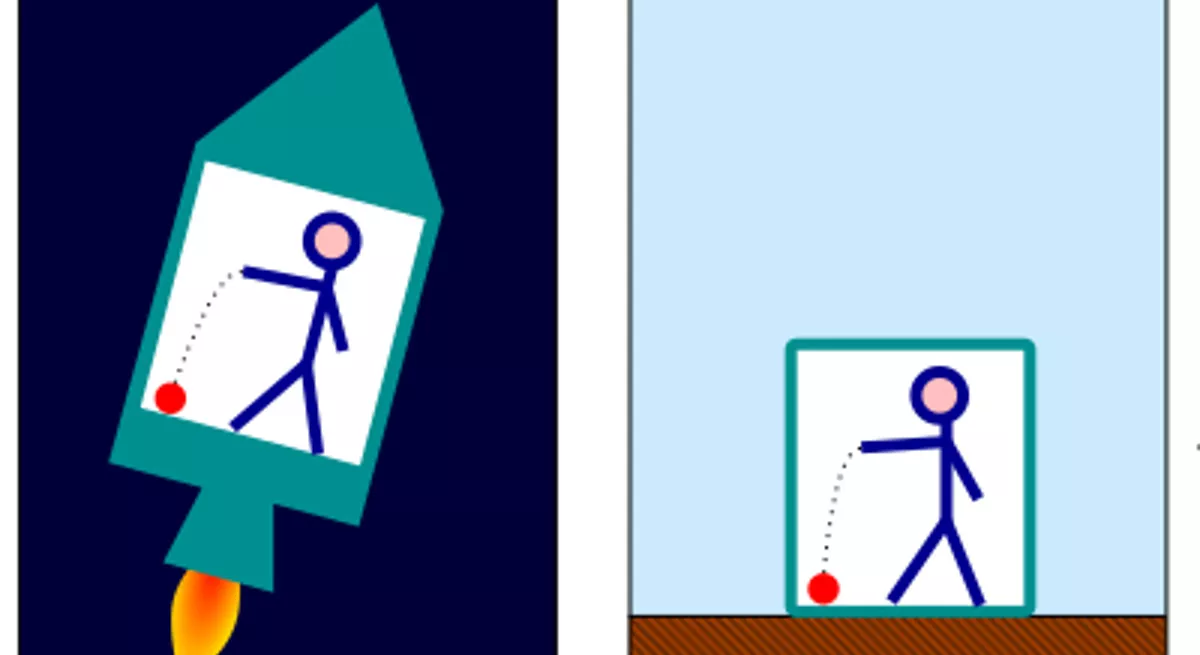
Son equivalente ambas situaciones para la persona en el ascensor?

Experimento del ascensor

Ahora, extendamos el análisis anterior al caso de un rayo de luz:

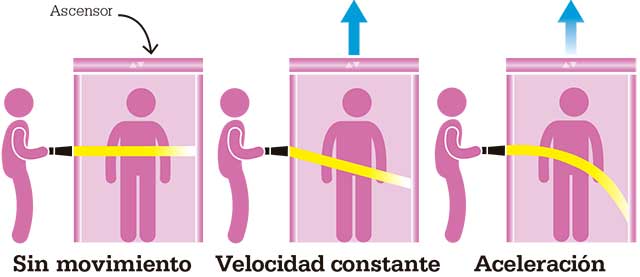
Experimento del ascensor

El Principio de Equivalencia de Einstein

En base a este experimento mental, Einstein postuló que:

Localmente, ningún experimento puede distinguir entre un campo gravitacional, y un sistema de referencia acelerado en ausencia de gravedad.

El Principio de Equivalencia de Einstein

De esta forma:

  • Se explica que la gravedad sí afecta la trayectoria de la luz.
  • Esto motiva el entender que la gravedad puede ser interpretada como un efecto geométrico en el espacio-tiempo.

Experimento del Eddington

---

## **Gravedad vs Aceleración**

- De lo anterior, podríamos concluir que podemos siempre utilizar la aceleración para detectar un campo gravitacional.

- Esto no es cierto en general.

---

## **Experimento del ascensor**

Imaginemos un observador dentro de un ascensor en caída libre en presencia de un campo gravitacional. Como tanto el ascensor como el observador están sujetos a la misma aceleración gravitacional:

$$ a = -\nabla \Phi $$

En tal caso, el observador no siente ninguna fuerza y experimenta un entorno "sin gravedad". Este es el **Principio de Equivalencia** en su forma más básica.