Ondas Gravitacionales pt 2

Clase 13

Objetivos de la Clase

• Discutir la detección de ondas gravitacionales y su importancia en astrofísica.
• Analizar el proceso de inspiral y su relación con el "chirp" de la señal gravitacional.
• Relatividad Numérica.

Ejemplo: Sistema Binario

• Consideremos un sistema de dos masas $m_1, m_2$ en órbita circular en el plano XY. Su momento cuadrupolar es:

  $$I_{ij} = \frac{1}{2} \mu R^2 \begin{bmatrix} 1 + \cos 2\omega t & \sin 2\omega t & 0 \\ \sin 2\omega t & 1 - \cos 2\omega t & 0 \\ 0 & 0 & 0 \end{bmatrix}$$

  donde:

  • $\mu = \frac{m_1 m_2}{m_1 + m_2}$ es la masa reducida del sistema.
  • $R$ es la separación orbital.
  • $\omega$ es la frecuencia angular orbital.

Pérdida de Energía por Emisión de Ondas

• Al orbitar, el sistema emite ondas gravitacionales y pierde energía.

• La tasa de emisión de energía se obtiene como el promedio temporal:

  $$L_{\text{GW}}\equiv - \frac{dE}{dt} = \frac{1}{5} \langle \dddot{\mathcal{I}}^{ij} \dddot{\mathcal{I}}_{ij} \rangle$$

• Esta expresión se conoce como formula cuadrupolar (similar a la electrodinámica).

Pérdida de Energía por Emisión de Ondas

• Para el sistema binario, esta expresión toma la forma:

  $$L_{\text{GW}} = \frac{32}{5} \frac{M^3 \mu^2}{R^5}$$

  donde $M = m_1 + m_2$ es la masa total.

• Esta pérdida de energía reduce el radio orbital y aumenta la frecuencia de la órbita.

• Inicialmente, el movimiento es casi perfectamente circular, y el radio cambia muy lentamente.

El Inspiral y la Señal "Chirp"

• Usando que para un movimiento circular $E=-1/2 M\mu/R$:

  $$\frac{dR}{dt} = - \frac{64}{5} \frac{M^2 \mu}{R^3}$$

• Aplicando al sistema binario la ley de Kepler $\Omega=(M/R^3)^{1/2}$ e integrando, se obtiene la frecuencia de la onda gravitacional:

  $$f_{\text{GW}} = \frac{5^{3/8}}{8\pi} \frac{1}{M^{5/8} (T-t)^{3/8}}$$

  donde $T$ es el tiempo de coalescencia.

El Inspiral y la Señal "Chirp"

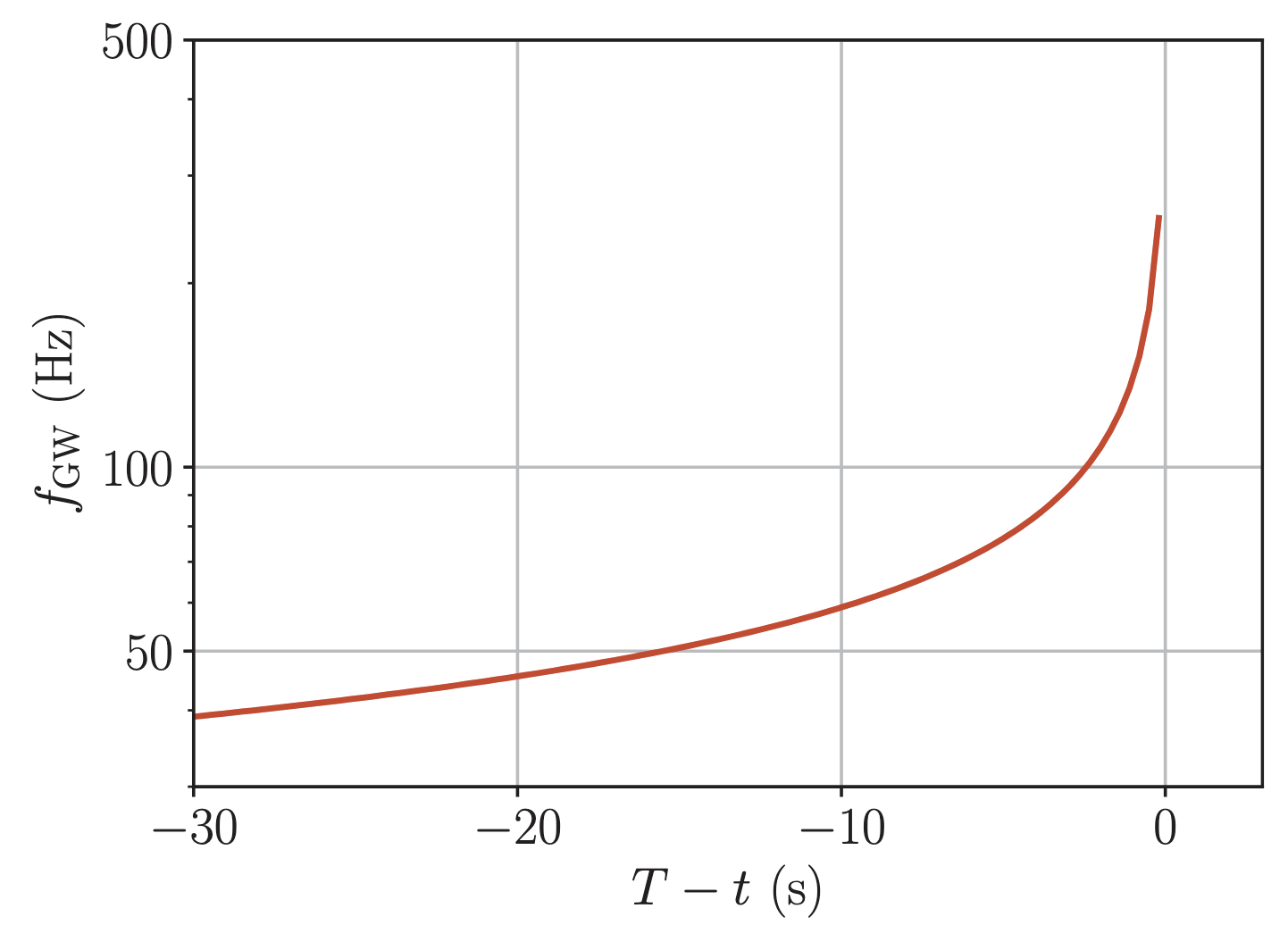
La Primera Detección de Ondas Gravitacionales: GW150914

• En 2015, LIGO detectó por primera vez ondas gravitacionales de la fusión de dos agujeros negros.
• El evento, llamado GW150914, confirmó directamente la predicción de Einstein.

El interferómetro de LIGO-Virgo

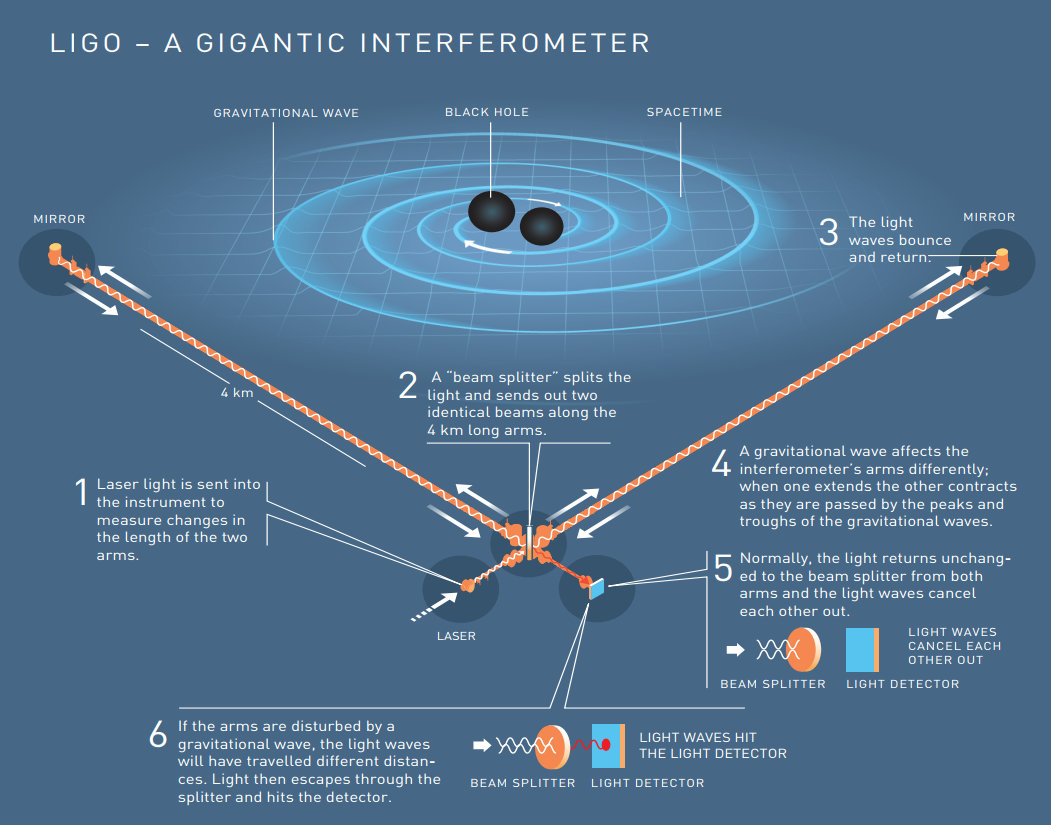
Detección de LIGO-Virgo

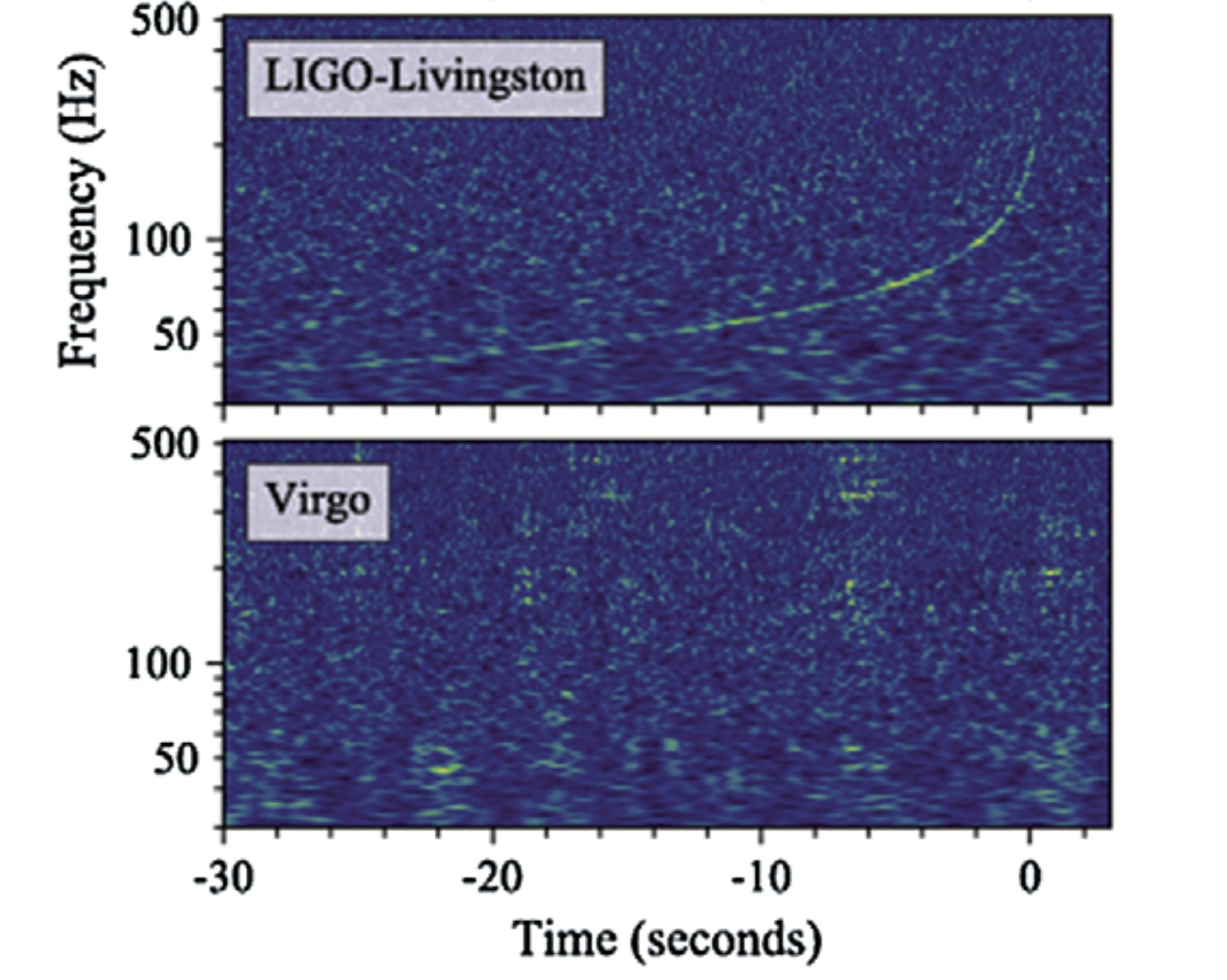
Más allá de las pertubaciones

• El resultado discutido asume que el sistema orbita lentamente, y por lo tanto la señal predicha describe una fase inicial del sistema.
• La señal observada por LIGO-Virgo corresponde a la emitida durante esa fase.
• Como es la dinámica del sistema a lo largo del tiempo, más allá de esta fase inicial?

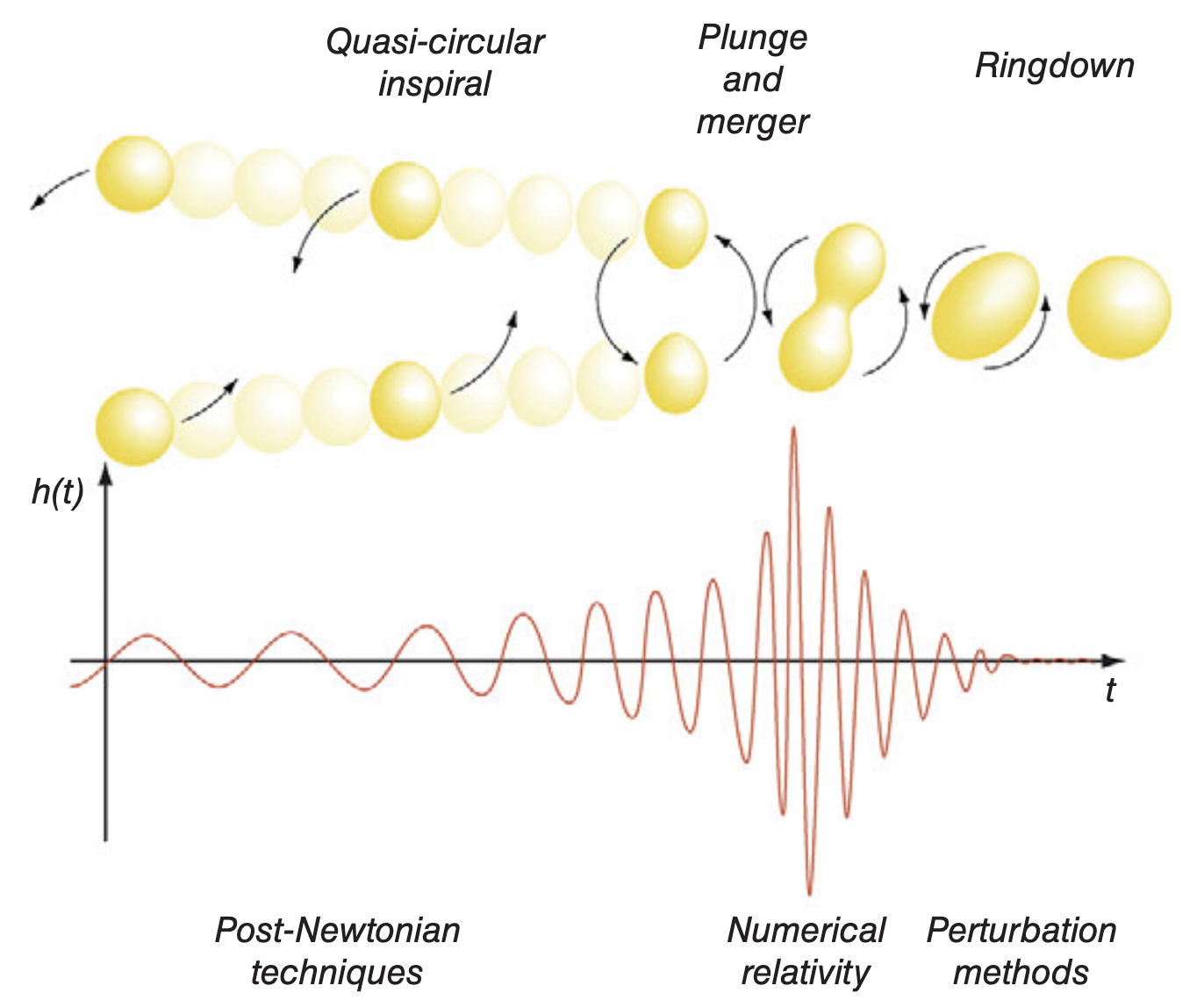
Más allá de las pertubaciones

• La señal que emite el sistema durante la etapa de merger no puede obtenerse mediante cálculos analíticos. Es necesario resolver las Ecuaciones de Einstein de forma numérica.

  • Esto es lo que llamamos Relatividad Numérica.

• Esto es altamente demandante técnica y computacionalmente.

  • Suele requerir supercomputadores.
  • Necesita cuidado con los métodos numéricos y errores.

• Sin embargo, es posible resolver numéricamente otros sistemas más simplificados (pero interesantes) de forma más modesta.

Relatividad Numérica

• Es posible resolver numéricamente las ecuaciones de la RG.
  • Por ejemplo, mediante el método de diferencias finitas aplicado a EDP.
• Sin embargo, existen algunos problemas con las EdE.
  • Es posible mostrar que los errores en la solución tienden a acumularse en el tiempo, incluso si inicialmente la solución es muy precisa.
• Una opción es escribir las EdE en una forma equivalente, pero que sea numéricamente más favorable.

Relatividad Numérica

• Esto no es siempre necesario. Pero sí lo es para algunos sistemas importantes, e.g. la colisión de agujeros negros o estrellas de neutrones.
• Esto se puede hacer con una formulación '3+1'.
• Veremos algo de esto en algunas clases más.
• Por ahora, nos detendremos a explorar un poco más las soluciones de las EdE que hemos visto.

Conclusion

• Las ondas gravitacionales surgen de las ecuaciones de Einstein en el régimen de campo débil.
• Su emisión sigue la fórmula del cuadrupolo y depende de la segunda derivada del momento de masa.
• Sistemas binarios pierden energía por ondas gravitacionales, provocando inspiral.
• La detección de GW150914 confirmó estas predicciones y abrió la era de la astronomía de ondas gravitacionales.