Inteligencia Artificial y Machine Learning

Hemos visto que el análisis de datos es de gran importancia en la ciencia. También hemos visto que, por la gran cantidad de datos disponibles actualmente, necesitamos nuevas técnicas de análisis. No es tan fácil hoy en día hacer los análisis en forma "tradicional":

• Explorar
• Gráficar
• Refutar/apoyar hipótesis

Hoy en día se necesitan algoritmos automáticos para hacer el análisis de datos, pero hay muchos tipos de análisis que no se pueden hacer muy fácilmente de manera automática.

Un ejemplo de la astronomía: clasificación de las galaxias

Las galaxias tienen distintas formas. Las dos categorías más amplias son "elíptica" o "espiral". Dentro de estas clasificaciones hay más subcategorías.

Elíptica	Espiral

Las subcategorías son:

Tradicionalmente, ¿Cómo se clasifican las galaxias? ¡Por la vista! Los astrónomos miran a las imagenes y deciden la categoría según su aparencia visual.

En los surveys de galaxias típicamente se observan millones de galaxias. No es factible que alguien mire cada imagen y clasifique todas las galaxias...

Pero ¿por qué es algo debe hacerlo una persona? Es porque los humanos son muy buenos en identificar objetos por su apariencia visual.

A veces demasiado buenos...

¿Nube o conejo?

Sólo un pan tostado? o la cara de Jesús?

Tiene sentido que una persona haga la clasificación de las galaxias. Una solución al problema de tener muchas imagenes de datos es pedir la ayuda de otros...

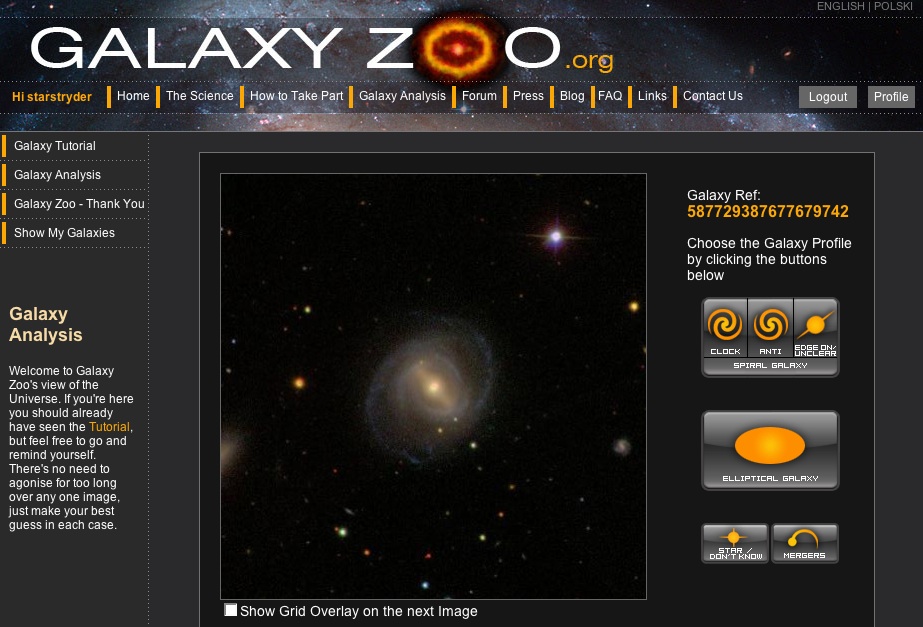
https://www.zooniverse.org/projects/zookeeper/galaxy-zoo

Este es un ejemplo de ciencia ciudadana donde cualquier persona puede ayudar a hacer nuevos descubrimientos en la ciencia y otros áreas.

https://www.zooniverse.org/projects

Hay proyectos en las artes, la biología, la historia, la literatura, la medicina, la física, etc.

¿Podría hacerlo también un computador?

La tarea de reconocer lo que hay en una imágen visual es algo que los humanos hacen sin pensar.

Para un humano esto es natural, pero en el fondo requiere:

• Contexto
• Criterio
• Tomar decisiones con información poco clara...

La Inteligencia artificial (IA) es el área de la informática sobre el desarrollo de los algorítmos que pueden lidiar estos desafíos (es decir, que permiten a un computador "pensar como un humano").

Sería demasiado complejo programar explícitamente todos los pasos que un computador necesitaría para reconocer una imagen.

• Sería mucho mejor si el computador pudiese aprender por si mismo como hacerlo.

Por eso, una parte muy importante de la inteligencia artificial es el diseño e implementación de algoritmos de aprendizaje de máquina (machine learning).

Inteligencia Artificial (IA)

La IA tiene una historia larga y complicada.

• Desde los primeros días de la informática se ha preguntado si un computador podría ser tan inteligente como un humano.

• El padre de la informática, Alan Turing, ideó una prueba para ver si una máquina tenía inteligencia o no - la famosa prueba (test) de Turing.

La prueba de Turing

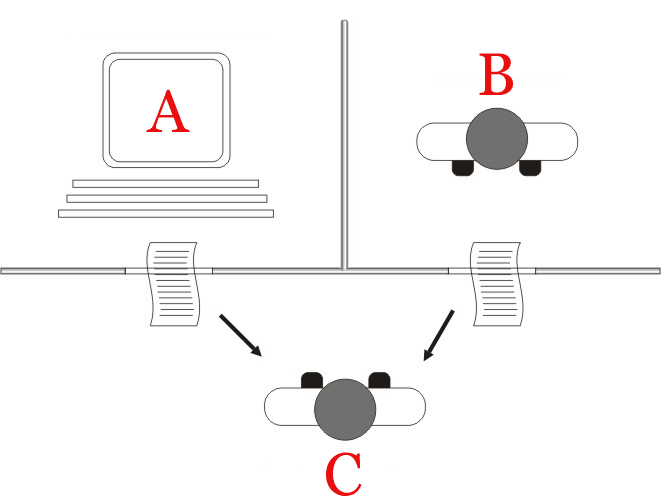
La idea de la prueba es la siguiente:

• Hay una persona $C$ que hace preguntas a $A$ y $B$.
• Escondidos de la persona $C$, hay un computador $A$ y otra persona $B$.
• Si la persona $C$ no puede determinar cuál de $A$ o $B$ es el computador, entonces decimos que el computador es "inteligente".

Aunque el concepto de la prueba es interesante, de hecho tiene muchos problemas:

1. No es muy objetivo: depende de la persona haciendo las preguntas, de las preguntas, etc.
2. Es específico a la inteligencia *humana*. Sabemos muy bien que muchas veces los humanos actuan sin inteligencia, y parece que hay otros animales que tienen mucha inteligencia.
3. Es la inteligencia "de verdad" o inteligencia "simulada"?

En la práctica, el resultado de la prueba, al final, ¡es irrelevante!

Una analogía:

• Nadie dice que el objetivo de la aeronáutica es construir aviones que vuelen de forma tan similar a los pájaros que ni los pájaros reales puedan distinguirlos!

Si bien la computación avanza, el objetivo no es precisamente el desarrollar computadores tan "inteligentes" que no podamos distinguirlos de los humanos...

La definición de la inteligencia

Entonces, la pregunta más fundamental, que la prueba de Turing no aborda, es ¿qué es la inteligencia?

La respuesta es típicamente "algo que actúa como nosotros, los humanos". Pero esta defición es muy vaga, y lógicamente circular.

A pesar de que no hay una definición buena de lo que es "la inteligencia", la historia de la IA incluye muchos intentos de construir una máquina con una inteligencia general, como un humano. Esta aún no existe.

IA moderna

Hay un punto de vista moderno de la IA que es diferente.

• En vez de crear un computador que "piensa como un humano", podemos intentar crear algorítmos que hacen cosas que, usualmente, los humanos han hecho mejor que el computador.

• Estas son cosas que involucran información incompleta, razonamiento probabilístico, inferencia, etc.

Ejemplo: reconocimiento de imágenes

De nuevo, el reconocimiento de imágenes es un ejemplo muy común. En esta imágen es muy fácil para nosotros ver que hay una bici roja:

...pero es muy difícil (sin las técnicas de machine learning) escribir un algorítmo que puede identificar los contenidos de cualquier imágen.

Por cierto, el concepto de una "captcha" es para asegurar que el usuario es una persona y no un computador (un "bot"):

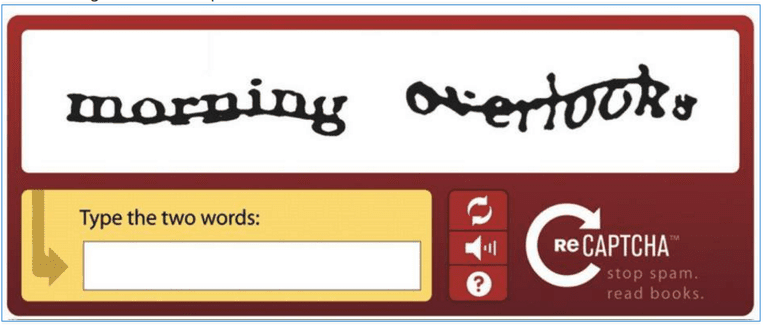
Es muy fácil (para nosotros) leer la palabra, pero típicamente es muy difícil para un computador (especialmente cuando esta distorcionada como en el ejemplo).

Ejemplo: Lenguajes Naturales

En la computación se denominan lenguajes naturales al que hablan los humanos (e.g. castellano, inglés), para poder distinguirlos de los lenguajes de programación.

Al contrario que los lenguajes de programación:

• Los lenguajes naturales tienen mucha ambigüedad.
• Uno necesita saber el contexto de una frase para entenderla...

El área de los lenguajes naturales es muy importante hoy en día en el área de las IA, e.g. ChatGPT.

Hay varias áreas de investigación en el área de lenguajes naturales en IA:

• Natural Language Processing: Procesamiento de los lenguajes naturales, por ejemplo en el uso de asistentes virtuales, traducción automática (Google Translate).
• Natural Language Understanding: Entendimiento de los lenguajes naturales, por ejemplo tener una máquina que puede entender el contenido de una noticia.
• Natural Language Generation: Generación de los lenguajes naturales, por ejemplo los chatbots que responden a preguntas, o un programa que puede redactar una carta.

Aplicaciones de IA

Existen tres tipos de aplicaciones fundamentales de la inteligencia artificial:

• Clasificación: categorizar lo que existe en el mundo.
• Predicción: anticipar lo que va a pasar en el futuro.
• Reacción: responder a las circunstancias actuales.

Classificación

Para entender el mundo, tenemos que organizar nuestro conocimiento del mismo: tenemos que clasificar (categorizar) lo que hay.

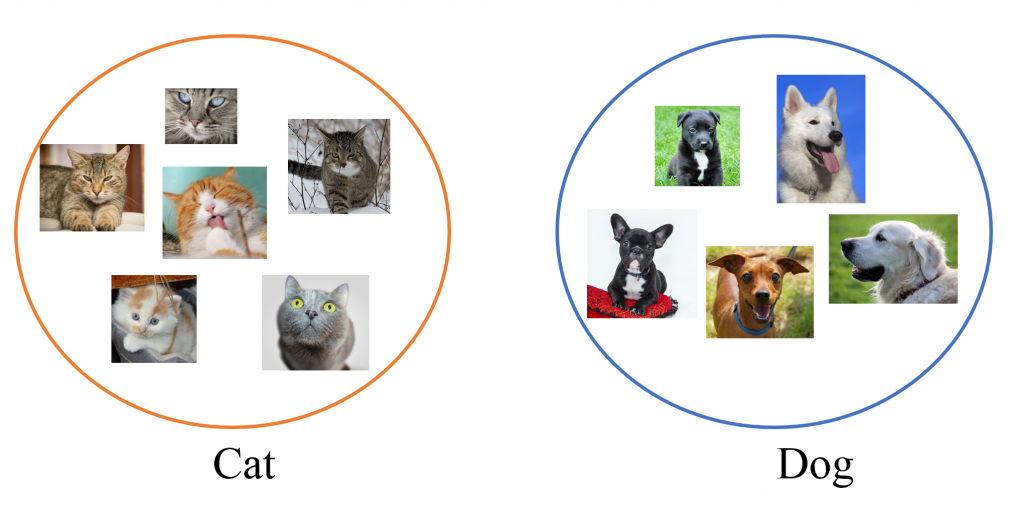
Predicción

Es importante para nosotros tener la capacidad de anticipar más o menos lo que va a pasar en el futuro (el futuro inmediato).

• Clima.
• Desastres naturales.
• Movimiento de acciones en mercados bursátiles.
• Crisis económicas/sociales.
• ...

Típicamente esto se ha trabajado con modelos matemáticos, pero hoy en día también puede hacerse en combinación con las IA...

Reacción

En el caso de un sistema inteligente, es importante reaccionar a los eventos externos.

Por ejemplo, un vehículo autónomo obviamente tiene que reaccionar bien a eventos externos...

Este aspecto de la inteligencia artificial tiene más relevancia para los robots que para los sistemas típicamente utilizados en la ciencia.

A la derecha: Robot de Boston Dynamics.

IA aplicada a la ciencia

Una aplicación de la IA hoy en día es el diseño de algorítmos para la extracción de información útil de datos complejos, incompletos e inciertos.

En la ciencia, podemos usar estos algorítmos para muchos tipos de análisis:

• Clasificación.
• Identificación de datos raros (outliers).
• Determinación de relaciones entre variables.
• Predicciones para observaciones futuras.
• y mucho más...

Hablamos de algorítmos de *machine learning*: un conjunto de técnicas diseñadas para lidiar este tipo de problemas.

Se llama machine learning (aprendizaje de máquina) porque los algorítmos pueden mejorar su propio rendimiento con más y más datos, es decir aprenden.

Tipos de machine learning

Hay dos tipos principales de machine learning:

1. Aprendizaje sin supervisión.
2. Aprendizaje con supervisión.

También hay aprendizaje semi-supervisado (entre supervisado y no supervisado) y aprendizaje reforzado (más para robots/agentes).

Aprendizaje sin supervisión

Estos son algorítmos que podemos aplicar a los datos inmediatamente, sin la necesidad de "entrenamiento".

Un ejemplo simple es un algorítmo que se llama k-means clustering.

Ejemplo: Clasificación de estrellas

Las estrellas pueden clasificarse en base a su temperatura y masa:

• Las estrellas en la secuencia principal tienen masas y temperaturas bajas,
• Las gigantes rojas tienen masas y temperaturas mayores.
• Las gigantes azules tienen altas masa y temperaturas aún mayor.

Supongamos que tenemos mediciones de las masas y temperaturas de algunas estrellas:

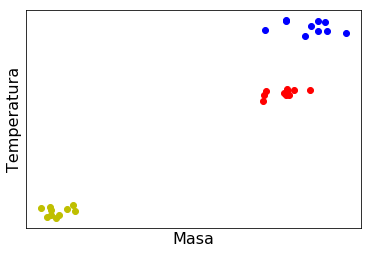
Tenemos un espacio de dos parámetros: masa y temperatura. Los datos agrupan en ciertas regiones de este espacio.

k-means clustering

Visualmente es muy fácil reconocer las regiones del espacio (bidimensional) de parámetros donde los puntos se agrupan.

Ahora, veremos que el algorítmo k-means clustering puede identificar estas regiones automáticamente.

datos = np.load("clase3_imagenes/datos.npy")

Importamos el módulo scikit-learn que contiene funciones que son implementaciones de muchos algorítmos de machine learning.

from sklearn.cluster import KMeans

Ahora vamos a usar el método k-means clustering. Suponemos que hay $3$ grupos de puntos (clusters). La función KMeans crea un objeto que podemos usar con nuestros datos.

kmeans = KMeans(n_clusters=3, n_init=10)

Aplicamos nuestro modelo de k-means a los datos que tenemos.

kmeans.fit(datos)

KMeans(n_clusters=3, n_init=10)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Podemos ver las posiciones de los centros de los grupos, según el algoritmo:

kmeans.cluster_centers_

array([[ 98.73404627, 101.08138838],
       [ 12.12593034,  12.23503402],
       [108.56303493, 150.63381276]])

El algoritmo indica cual punto está en cual grupo con una etiqueta (label):

kmeans.labels_

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2], dtype=int32)

Podemos usar estos números en la función scatter que grafica los datos. Uno de los argumentos de scatter es "c", para especificar el color de cada punto.

scatter(datos[:,0], datos[:,1], c=kmeans.labels_)
show()

El algoritmo ha identificado correctamente los distintos grupos de puntos!

Es importante notar que no hemos dado información sobre los datos: solamente que estamos buscando $3$ grupos. El algorítmo aprendió cuales son los grupos.

Este algoritmo es muy útil si queremos identificar grupos en muchos datos.

Por ejemplo, en vez de $30$ puntos, quizás tenemos $10000$ estrellas, y mediciones de $8$ variables, y no solamente $2$. Entonces, estaríamos buscando varios grupos dentro de los $10000$ puntos en un espacio con $8$ dimensiones! Vemos entonces que un algorítmo automático ayuda muchísimo.

Aprendizaje con supervisión

El ejemplo anterior era de un método "sin supervisión":

• No teniamos que dar datos de "entrenamiento" para enseñar el algorítmo.
• Es decir, el algoritmo se aplicó a nuestros datos en forma directa.

Ahora veamos un ejemplo de un algorítmo con supervisión, donde tenemos que enseñar al algorítmo con algunos de los datos.

Ejemplo: árbol de decisión (decision tree)

Árbol de decisión: Es como un diagrama de flujo. El algorítmo divide los datos según sus propiedades hasta que sean totalmente categorizados.

• Pero, el algoritmo necesita saber cuales propiedades corresponden a cuales categorías - por lo tanto hay que "entrenar" el algoritmo antes.
• Usamos datos que ya están categorizados (datos de entrenamiento), y el algorítmo se ajusta hasta que funcione bien con estos datos.

Después, podemos aplicar el algorítmo a datos nuevos.

Ejemplo: clasificación (taxonomía) de animales.

Tenemos un conjunto de datos (observaciones) que son las características de algunos animales.

Supongamos que tenemos observaciones de caballos, perros, vacas y pelícanos.

Observaciones	Caballo	Perro	Vaca	Pelícano
4 patas?	Si	Si	Si	No
Tiene pelaje?	No	Si	No	No
Tiene ubres?	No	No	Si	No

De las observaciones podemos determinar qué animal es usando un árbol de decisión:

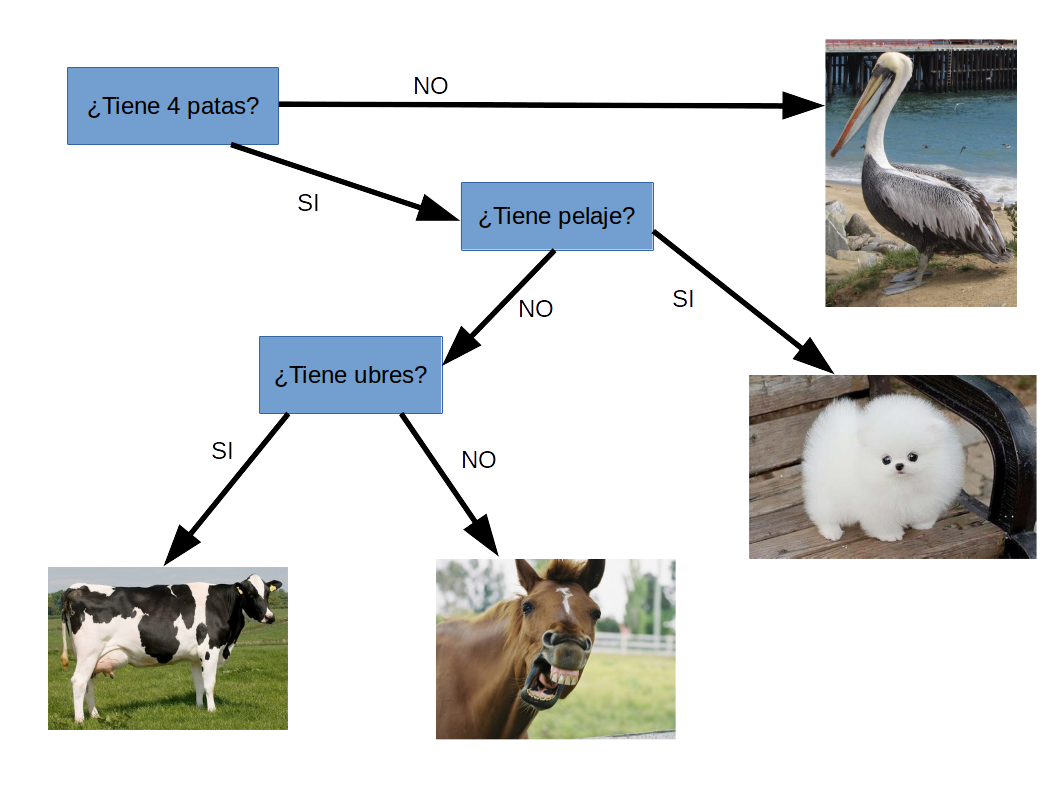
Ahora tenemos una clasificación de los datos según el árbol.

Con datos científicos, podemos construir el árbol en forma automática usando un algorítmo computacional.

De nuevo, el módulo de scikit-learn en Python contiene funciones para esto.

Árbol de decisión: las flores iris

En la botánica, las flores iris se clasifican de acuerdo a las dimensiones de sus pétalos y sépalos en tres especies.

• Iris setosa: Tamaño pequeño
• Iris versicolor: Tamaño mediano.
• Iris virginica: Tamaño mayor.

Un set de datos de flores iris viene disponible en el módulo scikit-learn.

Cargamos el módulo scikit-learn y los datos de flores iris:

from sklearn import tree
from sklearn.datasets import load_iris
iris = load_iris()

print("Especies:", iris.target_names)
print("Características:", iris.feature_names)

Especies: ['setosa' 'versicolor' 'virginica']
Características: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

print("Algunos de los datos:")
for i in range(5):
    print(f"Flor {i+1}: {iris.data[i]} (Clase: {iris.target[i]}, Especie: {iris.target_names[iris.target[i]]})")

Algunos de los datos:
Flor 1: [5.1 3.5 1.4 0.2] (Clase: 0, Especie: setosa)
Flor 2: [4.9 3.  1.4 0.2] (Clase: 0, Especie: setosa)
Flor 3: [4.7 3.2 1.3 0.2] (Clase: 0, Especie: setosa)
Flor 4: [4.6 3.1 1.5 0.2] (Clase: 0, Especie: setosa)
Flor 5: [5.  3.6 1.4 0.2] (Clase: 0, Especie: setosa)

Ahora clasificaremos las flores con el modelo en tres pasos:

1. Se entrena con los datos para que identifique patrones en ellos.
2. Con dichos patrones, inferirá como distinguir una especie de otra.
3. Construirá un árbol de decisión en base a las reglas que infirió (de forma automática).

arbol = tree.DecisionTreeClassifier()
arbol = arbol.fit(iris.data, iris.target)

Visualizamos el árbol construido en baso a lo que aprendió:

import graphviz

dot_data = tree.export_graphviz(arbol, out_file=None, 
                         feature_names=iris.feature_names,  
                         class_names=iris.target_names,  
                         filled=True, rounded=True,  
                         special_characters=True)

graph = graphviz.Source(dot_data)

graph

Redes neuronales artificiales

Un algoritmo más complejo en el área de machine learning es una Red Neuronal Artificial (RNA).

La investigación de las RNA comenzó hace muchos años en los primeros días de la Inteligencia Artificial.

La idea básica es crear un modelo computacional de algo similar a la estructura del cerebro:

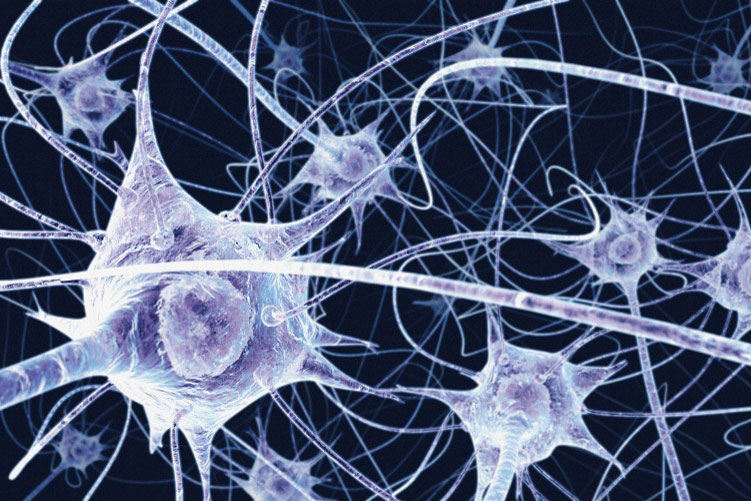
Una neurona en el cerebro se activa cuando recibe un señal suficientemente fuerte (un pulso eléctrico) de otras neuronas que están conectadas a sus dendritas.

Cuando la neurona se activa, manda un pulso eléctrico a lo largo de su axón que termina en sinapsis que se conectan con las dendritas de otras neuronas.

En la práctica, la neurona recibe entradas (impulsos eléctricos) y entrega salidas (impulsos eléctricos).

Esto es parecido a una función matemática:

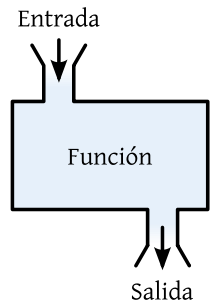
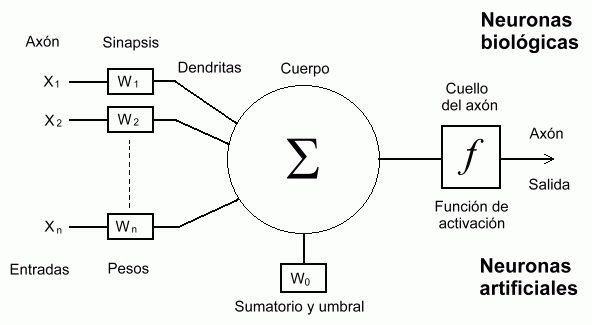
Una red neuronal artificial es un modelo muy simplificado de esta estructura cerebral. Las neuronas artificiales son así:

Neurona de McCulloch-Pitts

En este modelo, la neurona recibe "señales" en sus dendritas, que son simplemente los números $x_n$ multiplicados por pesos $w_n$.

Luego, en el cuerpo de la neurona se calcula la sumatoria (y a veces se agrega un valor de umbral).

El resultado de la sumatoria va como entrada a la función de activación $f$.

Podemos elegir (casi) cualquier función para la función de activación $f$. Algunas posibilidades son:

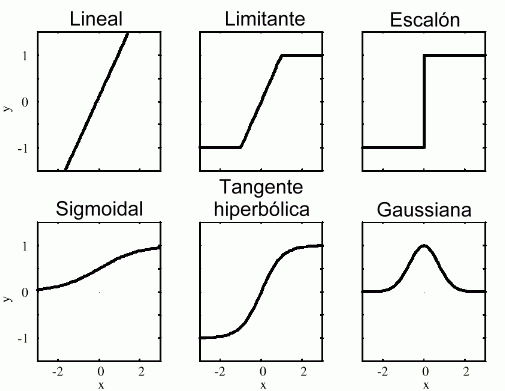
El resultado de la función de activación es la salida de la neurona, que puede ir como entrada a otra neurona, y así formar una red compleja.

Un ejemplo:

Una neurona recibe $4$ valores de entrada: $x_1 = 1$, $x_2 = -3$, $x_3 = -4$, $x_4 = 2$. Los pesos son $w_1 = 0.1$, $w_2 = 0.3$, $w_3 = 0.1$ y $w_4 = 0.5$. El sumatorio, usando los pesos, será:

$$x_1 w_1 + x_2 w_2 + x_3 w_3 + x_4 w_4 = -0.2$$

Supongamos que función de activación $f$ es la función escalón en los ejemplos arriba. Su valor de entrada es $-0.2 < 0$ así que su valor de salida es $-1$.

Por otra parte, si el valor de un peso fuese $w_1 = 0.5$ en vez del valor del ejemplo anterior, el sumatorio será igual a $0.2 > 0$ y la salida de la función de activación será $+1$.

Podemos contectar varias neuronas y así formar una Red Neuronal.

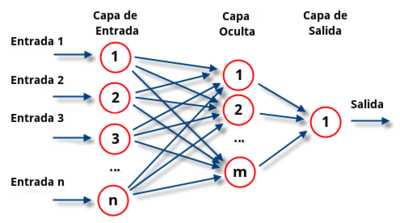
En el caso de una red:

1. Ingresamos valores de entrada a la primera capa de neuronas, que se llama la capa de entrada.
2. Las salidas de las funciones de activación de las neuronas en la primera capa dependen de los valores de entrada.
3. Estas salidas van como entrada a la próxima capa de neuronas. Ya que esta capa no está conectada al mundo "exterior" de la red, se llama una capa oculta.
4. Las salidas de la capa oculta van como entradas a la capa de salida, y las salidas de esta última capa son corresponden a las salidas finales de la red.

Mientras más capas ocultas tenga una red, más poderosa y compleja es.

• Antes mencionamos que las redes neuronales artificiales son como las funciones matemáticas.

• Pero, una red neuronal artificial puede aprender y mejorar su propio rendimiento! ¿Cómo lo hace?

Aprendizaje de la red

Cada conexión (sinapsis) entre las neuronas tiene asociado un peso. Este es un valor (típicamente) entre $0$ y $1$. Un valor de $0$ significa que esta conexión no contribuye nada la activación de la neurona. Un valor de $1$ significa que esta conexión tiene una contribución máxima a la activación de la neurona:

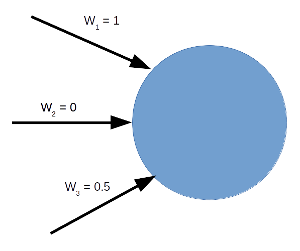
La activación o no de cada neurona depende de los valores de los pesos. El resultado final (la salida final) de la red depende del patrón de activación de toda la red.

• Podemos usar datos conocidos para ajustar los pesos para obtener la salida que queremos. Este proceso se llama entrenamiento de la red.

Por ejemplo, supongamos que tenemos una red neuronal con $3$ entradas. Damos los valores $3.1$, $-0.1$, $2.6$ como entradas a la red. Las salidas que queremos son $0$ y $1$ (hay dos neuronas en la capa de salida de esta red).

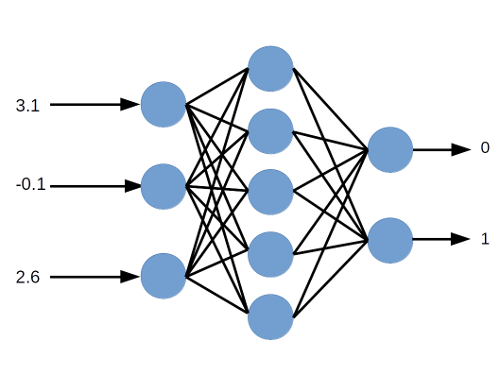
¿Cómo podemos garantizar que tendremos las salidas correctas? Ajustando los pesos.

Una red neuronal muy básica

Ahora vamos a crear una red neuronal para ver como funciona, y como podemos ajustar los pesos para obtener las salidas que queremos.

En este ejemplo, vamos a tener una "red" muy simple, que contiene solamente $1$ neurona, con $3$ sinapsis (entradas) y una salida:

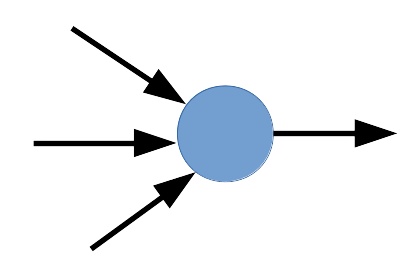
Queremos una red que pueda representar los siguientes valores de entrada y salida:

Entradas	Salida
0 0 1	0
1 1 1	1
1 0 1	1
0 1 1	0

Utilizaremos esto para entrenar la red.

Posteriormente, preguntaremos ¿cuál será la salida para las siguientes entradas?

Entradas	Salida
1 0 0	?

• Si nos fijamos bien, en nuestros datos de entrenamiento hay un patrón (oculto): la salida siempre es igual a la primera entrada.

• Luego, la salida debería ser $1$.

El primer paso es entrenar la red con los datos conocidos, i.e. determinar los pesos de cada entrada.

• Podemos comenzar el proceso utilizando pesos aleatorios.
• Después actualizamos los valores de los pesos hasta tener las salidas correctas.

Generamos $3$ pesos iniciales al azar (uno para cada entrada de la neurona):

pesos = random.uniform(low=0.0,high=1.0,size=3)
pesos

array([0.29272054, 0.29792714, 0.92678193])

El proceso de entrenamiento:

1. Elegimos un conjunto de entradas (por ejemplo, la primera fila de la tabla arriba).
2. Aplicamos los pesos a estos valores para calcular el sumatorio ponderado de las entradas.
3. Utilizamos el resultado del sumatorio como entrada a la función de activación $f$ de la neurona.
4. La salida de la función de activación, en este caso, es la salida de la red. Comparamos esta salida con el valor correcto y calculamos el error.
5. En este caso, el error es la diferencia entre la salida de la neurona y la salida correcta.
6. Ajustamos los pesos.
7. Repetimos el proceso muchas veces...

Paso 1

Elegimos la primera fila de entradas. Entonces tenemos $x_1 = 0$, $x_2 = 0$, $x_3 = 1$.

Paso 2

Sumatorio ponderado de las entradas: $x = \sum_i w_i x_i = w_1 x_1 + w_2 x_2 + w_3 x_3$.

entradas = array([0,0,1])
pesos*entradas

array([0.        , 0.        , 0.92678193])

Es conveniente notar que podemos representar las entradas y los pesos como vectores $\vec{x}$, $\vec{w}$.

sumatorio = sum(pesos*entradas)
sumatorio

0.9267819322375793

Pasos 3 y 4

La función de activación que vamos a ocupar en este caso es la función sigmoide: $y = \frac{1}{1+e^{-x}}$

La sigmoide es muy utilizada porque se parece a la función escalón (0 o 1), pero es más fácil derivar ya tiene una transición más suave, i.e. es siempre continua:

xvals = linspace(-6,6,100)
yvals = 1.0/(1.0 + exp(-xvals))
plot(xvals,yvals)
show()

Entonces, la salida de la función de activación en este caso es es:

1.0/(1.0 + exp(-sumatorio))

0.7164219534805756

Paso 5

Debemos comparar este resultado con la salida correcta, que es $0$.

El error en nuestra salida es la diferencia entre la salida correcta y la de la red:

$\epsilon = y_c - y$

(Hay varias maneras de calcular el error. Estamos usando una opción simple)

error = 0 - 1.0/(1.0 + exp(-sumatorio))
error

-0.7164219534805756

Paso 6

Ahora viene la parte más complicada. Queremos ajustar los pesos para mejorar el rendimiento de la red. En otras palabras, queremos reducir el error mediante un ajuste de los pesos.

Pensando en el problema en una forma matemática: lo que buscamos es el mínimo de la función que da el error. La operación de buscar este mínimo es algo que se llama optimización.

• De la aplicación del cálculo diferencial a este problema, es posible demostrar que la siguiente actualización de los pesos sirve:

$$\delta \vec{w} = \epsilon \vec{x} \frac{dy}{dx}$$

• Dado que para $y$ (que es la función de activación de la neurona) hemos escogido una sigmoide, su derivada es:

$$\frac{dy}{dx} = y(1-y)$$

$$\delta \vec{w} = \epsilon \vec{x} \frac{dy}{dx}$$

Esta ecuación nos dice que el ajuste de los pesos es:

• Proporcional al error $\epsilon$. Si el error es grande, implica que los valores de los pesos están muy lejos de sus valores óptimos, y por lo tanto deberíamos cambiarlos más que en el caso de un error pequeño.

• Proporcional a las entradas $\vec{x}$. Así que, cada peso es proporcional a la entrada asociada. Si la entrada asociada al peso es igual a cero, no importa que valor de peso tenemos y por lo tanto no es necesario cambiarlo.

• Proporcional a la derivada de la función de activación. Buscamos el mínimo del error, $\epsilon$. Este error esta dado por $\epsilon= y_c - y$. Para encontrar el mínimo de una función, hay que considerar su derivada. Entonces, la derivada del error es la derivada de la función $y$ ($y_c$ es una constante).

Es posible demostrar matemáticamente como actualizar los pesos para una red que tiene un número arbitrario de neuronas y conexiones.

Esta parte del algorítmo (la actualización de los pesos) es la parte más importante de la operación de una red neuronal artificial. El algorítmo para actualizar los pesos se llama *backpropagation*.

Es por el uso de backpropagation que la red puede aprender. Este es la diferencia entre una red neuronal artificial y una función matemática!

Ahora, calculamos la derivada:

y = 1.0/(1.0 + exp(-sumatorio))
derivada = y*(1-y)
derivada

0.20316153805165157

Entonces los cambios de los pesos son:

delta_w = error * entradas * derivada
delta_w

array([-0.        , -0.        , -0.14554939])

Actualizamos los valores de los pesos:

pesos += delta_w
pesos

array([0.29272054, 0.29792714, 0.78123255])

Calculamos el resultado con los nuevos valores de los pesos...

sumatorio = sum(pesos*entradas)
1.0/(1.0 + exp(-sumatorio))

0.6859456950655682

El valor ha reducido después de la actualización de los pesos. Hay que repetir el proceso varias veces, y también hay que ocupar todas los pares de entradas/salidas de entrenamiento:

Entradas	Salida
0 0 1	0
1 1 1	1
1 0 1	1
0 1 1	0

Entonces, vamos a aplicar el algorítmo a todas las entradas/salidas que tenemos.

entradas = array([[0,0,1],[1,1,1],[1,0,1],[0,1,1]])
salidas = array([[0,1,1,0]]).T   ## La "T" significa la transpuesta del arreglo

entradas

array([[0, 0, 1],
       [1, 1, 1],
       [1, 0, 1],
       [0, 1, 1]])

salidas

array([[0],
       [1],
       [1],
       [0]])

pesos = random.uniform(low=0, high=1.0, size=(3,1))

pesos

array([[0.84993761],
       [0.55092806],
       [0.90156574]])

Definimos una función en Python para la función de activación de la neurona.

def sigmoide(x):
    return( 1/(1+exp(-x)) )

Podemos calcular el sumatorio de cada conjunto de entradas con los pesos ocupando el producto escalar entre cada fila del arreglo "entradas" y el vector "pesos". En NumPy el producto escalar está dado por la operación dot:

y = sigmoide(dot(entradas, pesos))
y

array([[0.71127116],
       [0.90907821],
       [0.85214232],
       [0.81038194]])

Los errores son:

errores = salidas - y
errores

array([[-0.71127116],
       [ 0.09092179],
       [ 0.14785768],
       [-0.81038194]])

La derivada de la función de activación otra vez es $y(1-y)$:

derivadas = y*(1-y)
derivadas

array([[0.2053645 ],
       [0.08265502],
       [0.12599579],
       [0.15366305]])

Entonces, para calcular los cambios de los pesos $\delta \vec{w} = \epsilon \vec{x} \frac{dy}{dx}$ para cada fila de entradas podemos usar la operación "dot" de nuevo:

entradas.T

array([[0, 1, 1, 0],
       [0, 1, 0, 1],
       [1, 1, 1, 1]])

dot(entradas.T, errores * derivadas)

array([[ 0.02614459],
       [-0.11701062],
       [-0.24445102]])

Estos son los valores de $\delta \vec{w}$ que usamos para actualizar los pesos. Ahora, repetimos este proceso muchas veces ($10000$) para entrenar la red:

for iteracion in range(10000):
    # Calculamos para todas las entradas y pesos
    y = sigmoide(dot(entradas, pesos))
    errores = salidas - y
    derivadas = y*(1-y)
    pesos += dot(entradas.T, errores * derivadas)

pesos

array([[ 9.67289994],
       [-0.20837025],
       [-4.62927587]])

Ahora comparamos las salidas de la red, para cada fila de entradas, con los valores correctos:

sigmoide(dot(entradas, pesos))

array([[0.00966745],
       [0.99211795],
       [0.99359101],
       [0.00786337]])

Estos valores son bastante similares a los valores exactos:

Entradas	Salida
0 0 1	0
1 1 1	1
1 0 1	1
0 1 1	0

Si estamos conformes con estas respuestas, entonces hemos terminado de entrenar a la red.

Ahora... ¿Podrá nuestra red puede determinar el valor correcto para entradas que nunca ha visto? Queremos ver la siguiente salida:

Entradas	Salida
1 0 0	1

nuevas_entradas = array([1,0,0])

sigmoide(dot(nuevas_entradas, pesos))

array([0.99993704])

¡Esta respuesta está muy cerca del valor correcto, que es $1$! ✅ 🤖

Aplicaciones de las redes neuronales artificiales

Las redes neuronales artificiales son la base de muchas aplicaciones de Inteligencia Artificial y machine learning.

Si alguien habla de "deep learning" (aprendizaje profundo) se refiere al uso de RNAs.

En la red que vimos había solamente una neurona, así que no era una "red" de verdad.

Con varias tapas de varias neuronas, podemos tener una relación muy compleja (no-lineal) entre las entradas a la red, y las salidas.

Por eso, las RNAs son muy útiles para problemas de análisis de datos en la ciencia que son problemas muy no-lineales.

Fuera de la ciencia, las RNAs son la base de intentos de diseñar inteligencias artificiales que tienen el nivel de la inteligencia humana.

Las recomendaciones de videos en YouTube están determinadas por una red neuronal artificial...

Resumen

• La cantidad de datos que hay en la ciencia hoy en día requieren técnicas de análisis más allá de las "tradicionales".
• Con el desarrollo de algoritmos de machine learning hoy en día es posible automatizar muchos tipos de análisis que antes necesitaban una persona.
• Hemos visto algunos ejemplos de algorítmos de machine learning:
  • Con supervisión (redes neuronales, árboles de decisión)
  • Sin supervisión (k-means clustering)
• En Python hay varios módulos que son útiles en esta área, como scikit-learn.
• Hay nuevas herramientas como TensorFlow que ayudan en el diseño de redes neuronales.
• La importancia de estas herramientas va a seguir creciendo hacia el futuro!