Análisis y ciencia de datos

• La ciencia necesita de experimentación, es decir, datos.
• El método científico: hacer hipótesis, adquirir datos, analizar datos, refutar/apoyar hipótesis.
• En astronomía, meteorología, física, la cantidad de datos disponible (hoy en día) es enorme. ¿Cómo podemos analizarlos?

El propósito del análisis de datos

• Buscamos información dentro de los datos para apoyar o refutar una hipótesis científica.
• Este es la actividad fundamental de cualquier científico trabajando en un area empírica: e.g. astronomía, meteorología, física experimental, física computacional, etc.

¿Qué son los datos?

En general, los datos están compuestos de parámetros o cantidades que describen un sistema, o un aspecto del sistema que estamos estudiando. Por ejemplo:

• Para una estrella variable, podrían incluir la luminosidad de la estrella, su período de variabilidad, etc.

• Para un experimento de física de partículas, podrían incluir la taza de producción de una partícula específica.

• Para una simulación computacional de la atmósfera, podrían incluir la presión, la temperatura, y la densidad del aire, calculados por la simulación en ciertos puntos en la superficie de la Tierra, y en ciertos momentos.

Con un conjunto de datos, podemos comenzar con el análisis.

Utilizaremos de ejemplo un caso del clima, con datos de la temperatura global promedio mensual (dataset: HadCRUT4, del UK Met Office, https://crudata.uea.ac.uk/cru/data/temperature/).

Pasos principales del análisis de datos:

1. Explorar y procesar los datos.

2. Aplicar análisis

3. Visualizar el resultado.

1. Exploración de los datos

El primer paso es simplemente "mirar" a los datos (i.e. verificar el contenido del archivo de datos, hacer un gráfico simple). Es un paso importante pero frecuentemente olvidado...

Nuestros cerebros son muy buenos en procesar información visual, por lo tanto una imágen visual de los datos puede otorgar información útil inmediatemente. Podemos ver inmediatemente si hay distintos grupos de datos, o valores que son muy diferentes de los demás.

Por ejemplo, si tenemos observaciones de estrellas variables, y graficamos sus masas y sus períodos, quizás veremos uno o dos puntos que están muy lejos del resto del grupo:

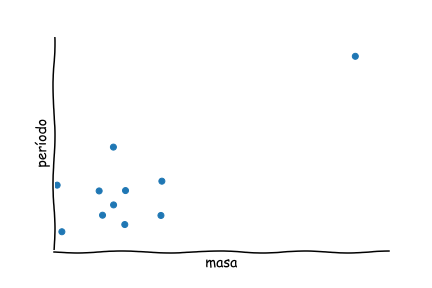
Puntos como estos se llaman outliers en inglés.

Podría ser que los datos tienen un error, o podría ser algo nuevo y interesante...

Veamos un ejemplo:

Tenemos un archivo de texto que contiene información del promedio global de la temperatura.

(Por simplicidad, el archivo de datos que viene de la página web ya está reducido.)

• Podemos leer las primeras 10 líneas del archivo desde Python con el comando "head" de Linux.
• Nota: para ejecutarlo desde el Jupyter notebook, anteponer "!".

!head clase2_imagenes_datos/HadCRUT.4.6.0.0.monthly_ns_avg_mod.txt

1850 01 -0.700
1850 02 -0.286
1850 03 -0.732
1850 04 -0.563
1850 05 -0.327
1850 06 -0.213
1850 07 -0.125
1850 08 -0.237
1850 09 -0.439
1850 10 -0.451

Aquí tenemos 3 columnas, la primera es el año, la segunda es el mes, y la tercera es la llamada anomalía en la tempertura promedio (diferencia respecto con al promedio de los años 1961-1990).

# Podemos ver todo el contenido del archivo con "cat":
# !cat clase2_imagenes_datos/HadCRUT.4.6.0.0.monthly_ns_avg_mod.txt

Mirando el contenido del archivo, al parecer no hay datos faltantes, ni valores muy grandes ni muy pequeños: los datos se ven "normales" ...

Ahora cargamos los datos en Python, y hacemos un gráfico simple:

datos = loadtxt("clase2_imagenes_datos/HadCRUT.4.6.0.0.monthly_ns_avg_mod.txt")
plot(datos[:,2])
ylabel("Anomalía de Temperatura")
show()

Vemos que existe una tendencia creciente, pero los datos todavía no están en la forma que realmente buscamos.

• Los datos contienen las temperaturas mensuales.
• Lo que nos interesa realmente es comparar año a año.
• Luego, es más conveniente ver los promedios anuales, para lo que necesitamos procesar los datos un poco.

# Seleccionamos los años únicos con la función "unique":
a = unique(datos[:,0])

promedio = []
for an in a:
    seleccion = (datos[:,0] == an)
    promedio.append( mean(datos[seleccion,2]) )

# Transformamos a un array de numpy (útil más adelante)
promedio = array(promedio)

plot(a, promedio)
xlabel("Año")
ylabel("Anomalía de temperatura")
show()

2. Aplicar análisis

Análisis de datos muchas veces significa un análisis estadístico, por ejemplo:

• Determinar el valor promedio de un parámetro.
• Determinar algo que se llama la desviación estándar ($\sigma$) de un parámetro.

Es muy importante tener conocimiento de la estadística para trabajar con datos! Hay un curso en el Semestre VI sobre Estadística.

La desviación estandar: es una medición de cuánto varía una variable. Si vemos a una parte del gráfico de temperatura donde los valores son más o menos "estables", vemos que hay desviaciones pequeñas de los valores.

La desviación estandar cuantifica cuanto se alejan los datos respecto al valor promedio ($\bar{x}$, o $\mu$).

La variación de un valor está asociada a la "distribución" del valor. Para muchas variables en la naturaleza la distribución es Gaussiana.

Por ejemplo, si medimos la temperatura corporal de cada persona en una ciudad, esta se representaría mediante una Gaussiana:

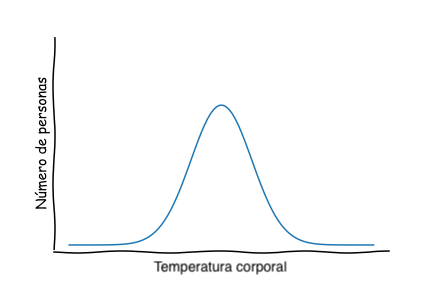
Este gráfico dice que una gran parte de la población tiene una temperatura corporal cernana al promedio, y muy pocas personas tienen temperaturas extremadamente altas o bajas.

Este tipo de función también se llama una función de densidad de probabilidad . Esta función da la probabilidad que una variable toma valores dentro de un cierto rango.

• La Gaussiana tiene dos parámetros: el promedio de la distribución, y la desviación estandar.

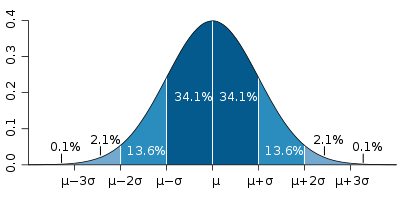
La desviación estandar ($\sigma$) determina el "ancho" de la distribución:

• Específicamente, incluye aproximadamente $68\%$ del área bajo la curva.

• Esto significa que $68\%$ de los valores medidos deberían estar "dentro de $1\sigma$" del valor promedio.

En el caso de las temperaturas en la Tierra, en la época de temperaturas estables, podemos considerar que las anomalías están distribuidas según la distribución Gaussiana.

Es un hecho estadístico que la combinación de errores en mediciones, variabilidad natural, etc. tenderán a causar que las variables tengan una distribución Gaussiana:

• Una desviación mayor que $1$ desviación estandar puede ocurrir en $32\%$ de los casos.
• Una anomalía mayor que $2$ desviaciones estandares puede ocurrir en sólo $5\%$ de los casos.
• Algo mayor que $3$ desviaciones estandares tiene una probabilidad de solamente $0.4\%$.

Análisis estadística de las temperaturas

Calculamos el valor de la desviación estandar para la época $1961-1990$ (referencia "estable").

# Convertimos el arreglo de años de "float" a "int"
a = array(a, int)

# Creamos un arreglo para elegir solamente las anomalías anuales para el
# período 1961-1990
seleccion = ((a <= 1990) & (a >= 1961))

La función std de NumPy calcula la desviación estandar de un conjunto de datos.

std(promedio[seleccion])

0.13215956816792848

Entonces, una anomalía anual de valor absoluto mayor que $\sim 0.132$ sería una anomalía mayor que $1$ desviación estandar.

Ahora calculamos los valores absolutos de las anomalías a partir del año 2000.

seleccion = (a >= 2000)
abs(promedio[seleccion])/0.132

array([2.24179293, 3.34722222, 3.76893939, 3.84532828, 3.39393939,
       4.13699495, 3.83143939, 3.72474747, 2.99305556, 3.8270202 ,
       4.24558081, 3.21843434, 3.56691919, 3.90088384, 4.39457071,
       5.78977273, 6.04356061, 5.12815657, 4.08712121])

Las anomalías a partir del año 2000 son mayor que $2\sigma$, y algunas son mayor que $5\sigma$!

Estas anomalías son tan improbables que no pueden ser variabilidad natural, aunque tenemos que tener en mente las suposiciones de nuestro análisis (por ejemplo, que el período $1961-1990$ es "estable").

3. Visualizar los resultados

Graficamos el valor absoluto de las anomalías a partir del año 1961, con una línea que indica $1$ desviación estandar del valor promedio de las anomalías en el período $1961-1990$.

seleccion = (a >= 1961)
plot(a[seleccion], abs(promedio[seleccion]))
plot([1961,2018],[0.132,0.132],'r-')
xlabel("Año")
ylabel("Anomalía de la temperatura")
show()

Con este gráfico podemos ver claramente que las anomalías de temperatura en los últimos $20$ años son mucho mayor que $1$ desviación estandar.

La visualización es una parte muy importante del análisis de datos. Ayuda con la comunicación del resultado, y a que otros investigadores pueden entender rápidamente nuestras conclusiones y sobre que base llegamos a ellas, y puedan verificar nuestros resultados.

Herramientas para análisis de datos

El trabajo de análisis de datos es lo que los astrónomos, los físicos experimentales, los meteorólogos, hacen todo el tiempo.

Hoy en día, tenemos muchas herramientas computacionales para este tipo de análisis.

En Python hay varios módulos útiles para análisis de datos:

• NumPy - Numerical Python (Python numérico)
• SciPy - Scientific Python (Python científico)
• matplotlib - Gráficos en Python
• pandas - Módulo para análisis de datos
• scikit-learn - Módulo para machine learning en Python

import pandas as pd

datos = pd.read_csv("clase2_imagenes_datos/Shapley_galaxy.dat", delim_whitespace=True)
datos.head()

/var/folders/x8/qmntmhgn3pz2c9r50zkbnt8c0000gn/T/ipykernel_88867/1691306055.py:3: FutureWarning: The 'delim_whitespace' keyword in pd.read_csv is deprecated and will be removed in a future version. Use ``sep='\s+'`` instead
  datos = pd.read_csv("clase2_imagenes_datos/Shapley_galaxy.dat", delim_whitespace=True)

	R.A.	Dec.	Mag	V	SigV
0	193.02958	-32.84556	15.23	15056	81
1	193.04042	-28.54083	17.22	16995	32
2	193.04042	-28.22556	17.29	21211	81
3	193.05417	-28.33889	18.20	29812	37
4	193.05542	-29.84056	12.55	2930	38

datos.describe()

	R.A.	Dec.	Mag	V	SigV
count	4215.000000	4215.000000	4215.000000	4215.000000	4215.000000
mean	201.591313	-31.544202	15.132287	14789.242942	59.873547
std	5.424458	2.252409	4.830717	8043.123152	49.745016
min	193.029580	-37.648890	0.000000	-75.000000	0.000000
25%	196.853335	-32.887360	15.140000	10937.000000	33.000000
50%	201.966670	-31.477500	16.200000	14483.000000	51.000000
75%	204.833750	-29.848055	17.720000	16578.500000	78.000000
max	216.030000	-27.503330	22.330000	76746.000000	899.000000

from pandas.plotting import scatter_matrix

plots = scatter_matrix(datos)
show()

Análisis de datos e Inteligencia Artificial

• La IA también es una herramienta muy útil para analizar datos.
• Hoy en día existen muchos módulos de Python con herramientas de IA.

Reconocimiento de escritura a mano

Utilizando herramientas de machine learning (aprendizaje de máquina), podemos lograr que el computador aprenda a reconocer la escritura a mano.

from sklearn import datasets, svm, metrics

# Cargamos un set de datos con imágenes de números
# Son de 8x8 pixeles cada una
digitos = datasets.load_digits()

# digitos.images tiene las imagenes.
# digitos.images tiene los numeros (respuestas).
imagenes_y_etiquetas = list(zip(digitos.images, digitos.target))
for index, (image, label) in enumerate(imagenes_y_etiquetas[:10]):
    subplot(3, 4, index + 1)
    axis('off')
    imshow(image, cmap=cm.gray_r, interpolation='nearest')
    title('%i' % label)

Usaremos estas imágenes como un conjunto de datos.

Para esto, las transformamos de 8x8 a 64x1.

n_muestras = len(digitos.images)
datos = digitos.images.reshape((n_muestras, -1))

# Usamos un algoritmo de machine learning que se llama 
# "support vector machine"
clasificador = svm.SVC(gamma=0.001)

Dividiremos nuestros datos en:

• Mitad para entrenamiento (aprendizaje)
• Mitad para las pruebas

# Usamos la mitad de los digitos (0-3) para "entrenar" el algoritmo
mitad_datos = n_muestras // 2
clasificador.fit(datos[:mitad_datos], digitos.target[:mitad_datos])

SVC(gamma=0.001)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Ahora le pediremos al clasificador que identifique imágenes con algunos de los números que no ha visto (4-9)

esperado = digitos.target[mitad_datos:]
predicho = clasificador.predict(datos[mitad_datos:])

imagenes_y_predicciones = list(zip(digitos.images[mitad_datos:], predicho))
for index, (image, prediction) in enumerate(imagenes_y_predicciones[:4]):
    subplot(2, 4, index + 5)
    axis('off')
    imshow(image, cmap=cm.gray_r, interpolation='nearest')
    title('Predic: %i' % prediction)

Parece que funciona bastante bien!

Para saber que tan bueno es el desempeño de nuestro clasificador, podemos pedir un reporte:

print(f"{metrics.classification_report(esperado, predicho)}\n")

              precision    recall  f1-score   support

           0       1.00      0.99      0.99        88
           1       0.99      0.97      0.98        91
           2       0.99      0.99      0.99        86
           3       0.98      0.87      0.92        91
           4       0.99      0.96      0.97        92
           5       0.95      0.97      0.96        91
           6       0.99      0.99      0.99        91
           7       0.96      0.99      0.97        89
           8       0.94      1.00      0.97        88
           9       0.93      0.98      0.95        92

    accuracy                           0.97       899
   macro avg       0.97      0.97      0.97       899
weighted avg       0.97      0.97      0.97       899

Si queremos algo más visual, podemos visualizar la "matriz de confusión":

disp = metrics.ConfusionMatrixDisplay.from_predictions(esperado, predicho)
disp.figure_.suptitle("Matriz de Confusión")
show()

Módulos para machine learning, diseñados para optimizar y evaluar expresiones matemáticas con arreglos. También aprovechan de los GPUs para acelerar el algoritmo.

Datos masivos

Anteriormente vimos que hoy en día tenemos muchos datos disponibles, pero demasiados para hacer un análisis "tradicional" como el que hicimos con las temperaturas.

Necesitamos nuevas técnicas de extracción, almacenamiento y análisis de datos. El desarrollo y aplicación de estas técnicas es una ciencia nueva que se llama ciencia de datos.

Bases de datos

Uno de los desafíos grandes en ciencia de datos es cómo almacenar y procesar los datos.

Un ejemplo es el nuevo telescopio Vera-Rubin LSST (en el norte de Chile).

• $\sim 15$ TB de datos por noche.
• No es factible tener todos estos datos en formato raw en un servidor.
• Por ejemplo, si quiero usar solamente los datos de estrellas variables, quiero buscar y descargar solamente esos datos, y no todos.

Por lo tanto, es muy importante construir una base de datos que guarda los datos en una forma estructurada y accesible.

Hay equipos que trabajan en la colaboración del LSST para diseñar su base de datos, y la infraestructura necesaria (servidores, conexiones, etc.)

Algunos otros ejemplos del uso de bases de datos:

• Las simulaciones cosmológicas modernas generan muchos datos que necesitan organización.
• Los experimentos en la física de partículas (por ejemplo, el LHC) también generan muchos datos.

Por lo tanto, para los científicos modernos es muy importante tener conocimiento del diseño y operación de las bases de datos.

Los tipos de bases de datos

• Relacionales: los datos están organizados en tablas, que tiene relaciones entre ellas. Es tipo más utilizado.

• No-relacional: bases de datos distribuidas, almacen de documentos, bases de datos gráficas, pares de valores-claves

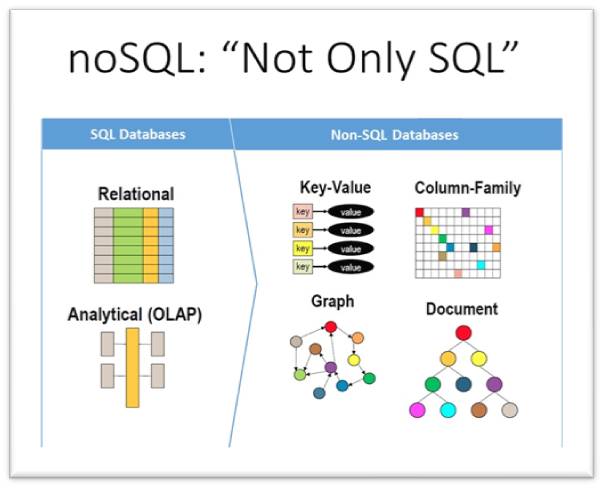
Bases de datos relacionales

Se puede "interactuar" con muchas bases de datos utilizando un lenguaje que se llama SQL (Structured Query Language). No es un lenguaje de programación, sino un lenguaje especializado para el uso de bases de datos.

• Los datos en una base de datos relacional están organizados en tablas (que a veces se llaman "relaciones") con columnas y filas.
• Las columnas corresponden a las atributas de los datos, mientra las filas son los registros.

Ejemplo: un catálogo de estrellas (filas), con coordenadas, tipo espectral, luminosidad, etc. (columnas):

Tabla: estrellas

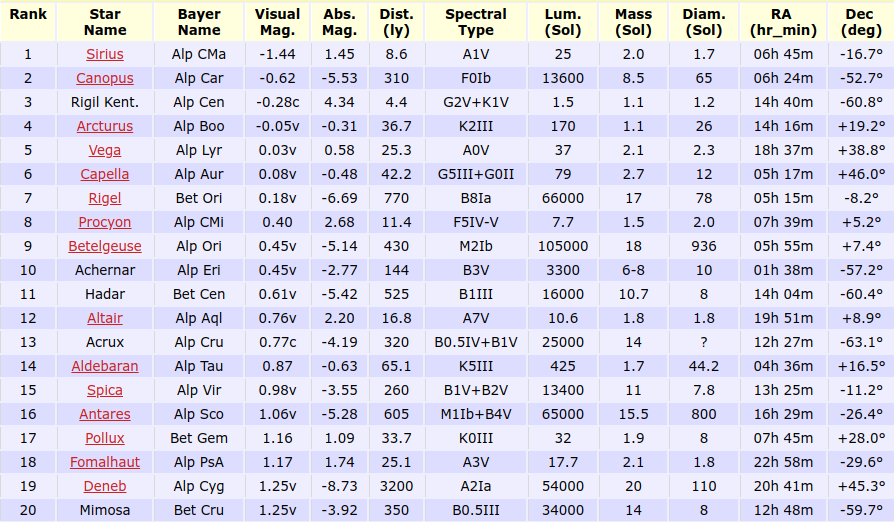
El punto importante es que cada fila tiene un número de identificación, o una clave.

Entonces, quizás tenemos otra tabla sobre estrellas variables, con atributas (columnas) acerca de la variación en magnitud, tipo de estrella variable, etc. Cada estrella en esa tabla también tendrá un número de identificación:

Tabla: estrellas_variables

ID	Nombre	Mag. max.	Mag. min.	Tipo
9	Betelgeuse	0.0	1.3	Supergigante rojo
60	Algol	2.1	3.4	Binaria eclipsante
61	Eta Carinae	-0.8	7.9	Variable LBV

Así que podemos relacionar las dos tablas por coincidencia de los números de identificación.

En esta manera podemos combinar la información de muchas tablas para encontrar lo que necesitamos.

Acceso remoto

En el caso de los datos masivos del LSST, por ejemplo, las tablas que contienen la información de las observaciones van a estar en un servidor (o varios).

Un astrónomo que quiere usar los datos puede enviar una solicitud al servidor (escrito en SQL) y el servidor combinará las tablas según lo que está pidiendo. Finalmente enviará la tabla resultante al usuario.

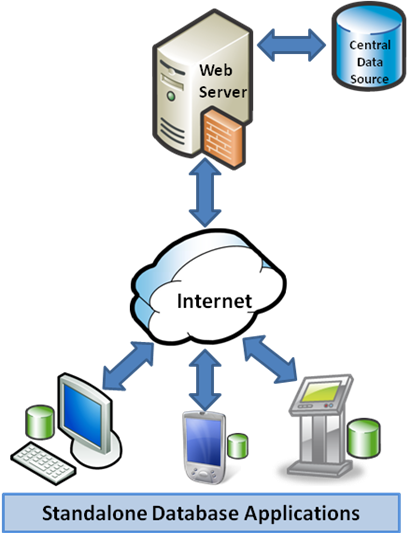
Bases de datos en la astronomía

Se puede acceder a muchos bases de datos astronómicas directamente de Python por el uso del módulo astroquery que es parte de astropy, un módulo de funciones útiles para la astronomía.

http://www.astropy.org/

https://astroquery.readthedocs.io/en/latest/

Análisis de datos masivos

Obtener los datos es el primer paso. El segundo es hacer el análisis!

Anteriormente vimos el ejemplo de la anomalía de temperaturas.

Ahora veremos un ejemplo que muestra las dificultades en trabajar con datos masivos.

Ejemplo: datos (imágenes) de pulsares

Un púlsar es una estrella de neutrones con una rotación muy rápida que emite en la longitud de onda de radio.

Suponemos que tenemos varias imagenes de pulsares.

• Podemos cargar la imágen a un arreglo, como vimos antes.
• Así que, tendremos los arreglos imagen1, imagen2, etc.

imagen1 = load("clase2_imagenes_datos/pulsars/image1.npy")
imagen6 = load("clase2_imagenes_datos/pulsars/image6.npy")

imshow(imagen1)
show()

<matplotlib.image.AxesImage at 0x30a011400>

imshow(imagen6)
show()

<matplotlib.image.AxesImage at 0x30a076c30>

Los datos de cada imágen están en arreglos de NumPy. Si las imágenes tienen una resolución de $200 \times 200$, vamos a tener arreglos de $200 \times 200 = 40000$ elementos.

Tenemos $10$ imagenes, así que cargamos todas las imagenes en un arreglos de $3$ dimensiones: $200 \times 200 \times 10 = 400000$ elementos.

imagenes = np.zeros((200,200,10))
for i in range(1,10+1):
    imagenes[:,:,i-1] = load("clase2_imagenes_datos/pulsars/image"+str(i)+".npy")

imagenes.shape

(200, 200, 10)

Combinando las imagenes

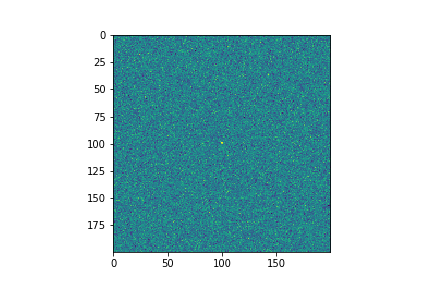
No se va nada en las imagenes! Solo "ruido"!

En cada pixel hay un "error" (ruido térmico en el detector, etc.).

Al parecer hay un "señal" (un punto muy brillante), pero no está muy clara debido al ruido en las imagenes...

Al igual que el ejemplo de las temperaturas, los valores en cada pixel ('brillo') parecen fluctuar.

Podemos usar la función histogram para calcular la frecuencia de ocurrencia de valores:

from scipy import stats
h, bins = histogram(imagenes.flatten(), density=True)
centros = 0.5*(bins[1:] + bins[:-1])

pdf = stats.norm.pdf(centros,loc=5.0)
scatter(centros, h)
scatter(centros, pdf)
ylabel("% de ocurrencias")
xlabel("Valor del pixel ('brillo')")
show()

• Del gráfico anterior, parece que los valores en los pixeles de las imagenes están distribuidas según la distribución gausiana, con valor promedio de $5$.
• Este valor corresponde al valor de fondo del instrumento (cuando está encendido, pero no observando nada).
  • Algo similar a una TV antigua encendida pero sin ningún canal en partícular.

¿Por qué es útil saber que los "errores" tienen una distribución gausiana?

• Porque ahora podemos "sumar" todas las imagenes, y los errores se van a cancelar (estadísticamente)!
• De hecho, calculemos el valor promedio de cada pixel con la funcion mean.

imagen_resultante = mean(imagenes,axis=2)

imshow(imagen_resultante)
show()

Ahora podemos ver un puntito en el medio que es la detección (estadística) de un púlsar!

Resumen

• Análisis de datos es algo que los científicos hacen todo el tiempo.
• Las herramientas computacionales que tenemos hoy en día ayudan muchisimo en ese área.
• El lenguaje Python tiene muchos módulos útiles para trabajar con datos.
• Con datos masivos, necesitamos una forma de organizarlos, por ejemplo con bases de datos.
• También hay que procesar (limpiar) los datos de problemas, errores, etc.
• En el análisis de datos masivos es necesario el uso de métodos nuevos (automáticos).
• En la mención hay $2$ cursos en el área de ciencia de datos. Las habilidades que uno aprende en esta área sirven para muchas áreas y trabajos.