Algoritmos
¿Qué es un algoritmo?
- Como vimos en la clase anterior, un algoritmo es como una receta: un conjunto de instrucciones para completar una tarea.
- Lo que el algoritmo hace no depende del lenguaje de programación (idioma).

¿Qué es un algoritmo?
- Es un conjunto prescrito de instrucciones o pasos bien definidos, cuyo fin es obtener una solución o resultado.
- La palabra viene del nombre del matemático, Mohammed ibn-Musa al-Khwarizmi, que formaba parte de la corte real en Baghdad, y vivió desde el año 780 hasta 850 (aprox).

Algoritmos
- Los algoritmos son independientes de los medios utilizados para completar la tarea.
- El mismo algoritmo podría implementarse con lapiz y papel, un computador, un abaco, etc.
- Por lo tanto, son independientes del lenguaje de programación que usamos.
- Un programa de computador es simplemente una implementación (o realización) de un algoritmo.
Precisión y rapidez de un algoritmo
- La precisión del resultado y la rapidez en obtenerla dependen del algoritmo usado.
- Si el algoritmo está diseñado mal, el problema será mucho más difícil de resolver.
- En general, evaluamos un algoritmo en términos de:
- Precisión del resultado obtenido.
- Rapidez para obtener el resultado.
Diseño del algoritmo
- El primer paso para resolver un problema computacionalmente es diseñar el algoritmo.
- Del mismo modo que un edificio no puede construirse sin un plan de arquitecto, deberíamos planificar nuestro método para resolver el problema antes de programar.
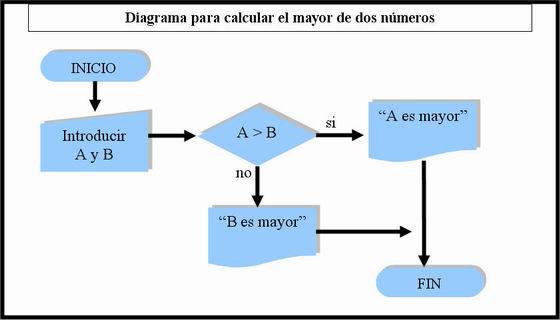
Diseño del algoritmo
- Lista de instrucciones
- Diagrama de flujo
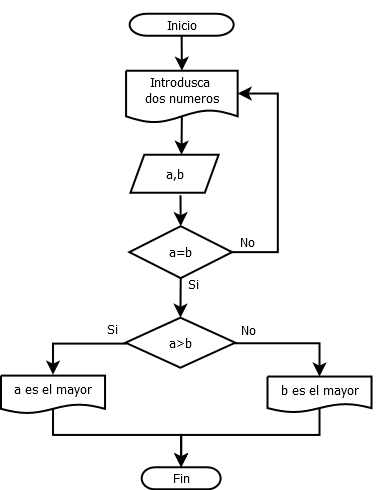
- Pseudo-código

Un ejemplo: ordenar números
- Dado un conjunto de números, queremos ordenarlos en orden ascendiente.
- ¿Cómo podemos hacer eso?

Un ejemplo: ordenar números
- No es necesario pensar en ningún lenguaje de programación específica cuando estamos diseñando un algoritmo!
- Primero, hay que pensar en los pasos lógicos que cualquier persona puede seguir para convertir una lista de números sin orden en una lista de números ordenados...

Un ejemplo: ordenar números
La opción más simple es ir tomando cada número de la lista y compararlo con todo el resto.
Sin embargo, existen formas más rápidas (con menos pasos) que nos llevaran al mismo resultado.

Un ejemplo de un algoritmo para ordenar números
Una posible solución a este problema es el siguiente algoritmo (que se llama "quicksort"):
Algoritmo Quicksort
- Elegir un elemento de la lista, que se llama el elemento pivote.
- Colocar todos los números menores que el elemento pivote a la izquierda, y todos los números mayores a la derecha.
- Para cada una de estas sublistas, realizar los pasos (1) y (2), e igualmente para cada sublista dentro de las sublistas, etc.
- Eventualmente las sublistas tendrán solamente $1$ elemento o ninguno, y estas sublistas estarán ordenadas por definición.
$\Rightarrow$ se trata de un algoritmo recursivo.
Quicksort
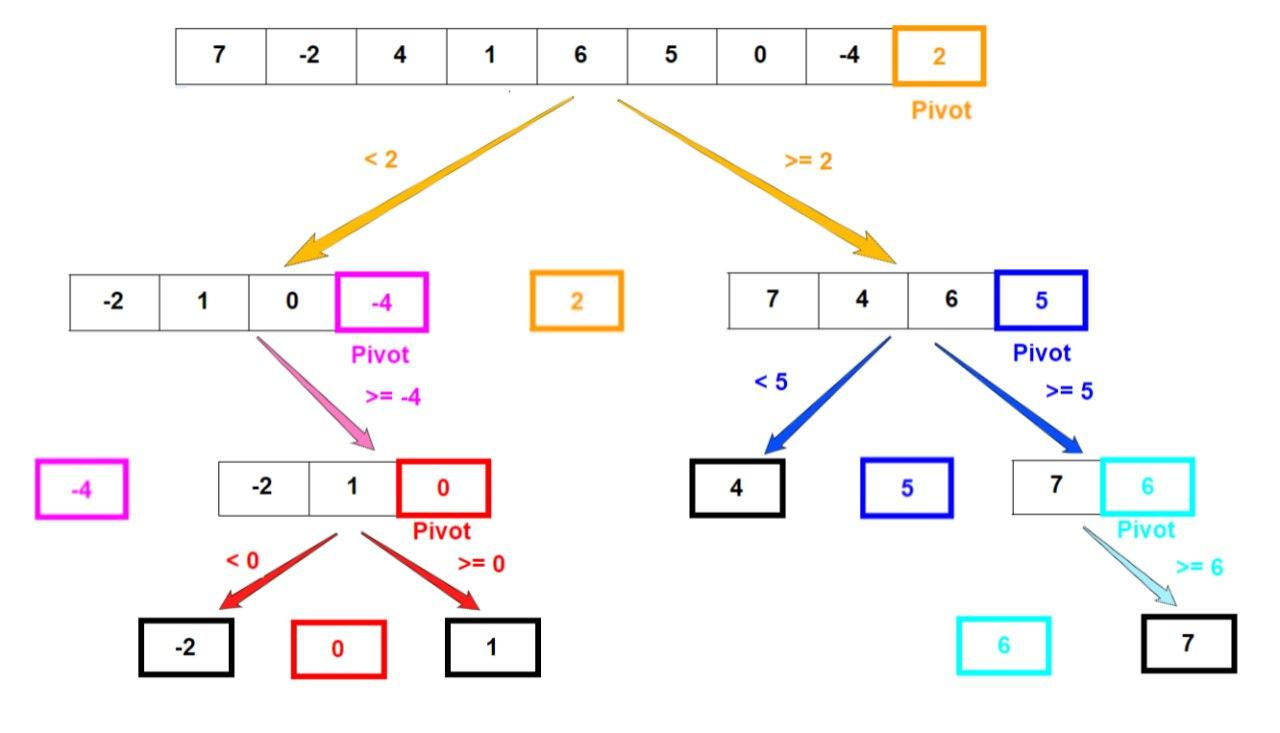
Eligiendo el mejor algoritmo
- ¿Cómo sabemos que el algoritmo que hemos diseñado es la "mejor" solución?
- ¿Qué significaría "mejor" en este caso?
- Típicamente significa el más preciso y el más rápido.
- Precisión es normalmente el primer aspecto de un algoritmo que verificamos.
- Calcular la rapidez de un algoritmo es un problema desafiante. ¿Cómo podemos comparar la rapidez de dos algoritmos?
Rapidez
Determinando la rapidez de un algoritmo
- Recordar que un algoritmo es independiente de los medios utilizados para implementarlo.
- Este significa que el algoritmo es independiente del computador que usamos y el lenguaje de programación.
- Por lo tanto, podemos caracterizar la "rapidez" de un algoritmo en una manera que no refiere a la velocidad del procesador, el número de procesadores, si usamos Python o C, etc.
Complejidad algorítmica
- En la computación, la rapidez de un algoritmo se define en términos de su complejidad algorítmica.
- Determinamos la complejidad de un algoritmo por la consideración del número de pasos que el algoritmo tiene que ejecutar para completar su tarea.
- Algoritmos que requieran más pasos serán más lentos (mayor complejidad algorítmica).
Complejidad algorítmica
- Pero, ¿qué es un "paso" para un algoritmo?
- NO es algo al nivel del procesador y sus ciclos de operación.
- En el análisis de algoritmos, estamos pensando al nivel de los cálculos necesarios en el algoritmo.
Complejidad algorítmica
- La complejidad algorítmica nos dirá como el algoritmo escala cuando lo aplicamos a más datos.
- En el caso de "quicksort" queremos saber que tan rápido o lento es el algoritmo cuando lo aplicamos a una lista de:
- $10$ elementos
- $100$ elementos
- $1000$ elementos
- ...
Por ejemplo, nos gustaría saber: ¿Cuantos pasos se requieren en el caso de $100$ vs $10$?
Complejidad algorítmica: N-cuerpos
- ¿Cómo describimos la complejidad de un algoritmo?
- Vamos a usar un algoritmo más simple que "quicksort".
- Analizaremos un tipo de simulación computacional que se usa mucho en la astrofísica: simulaciones de N-cuerpos.


Complejidad algorítmica: N-cuerpos
- El problema de N-cuerpos consiste en un sistema de N partículas sujetas a la acción de su propia gravedad (como el Sistema Solar).
- Fuerzas $\Rightarrow$ aceleraciones $\Rightarrow$ velocidades.
- Se puede actualizar las posiciones de las partículas con sus velocidades: el sistema se evoluciona en el tiempo.
Ejemplo: muchos planetas
Ejemplo: formación de la Luna
Complejidad algorítmica: N-cuerpos
- El "paso" básico en este algoritmo es el calculo de las fuerzas entre cada par de partículas.
- Con solo 2 partículas tenemos que calcular solamente la fuerza entre un par y listo! (1 paso).
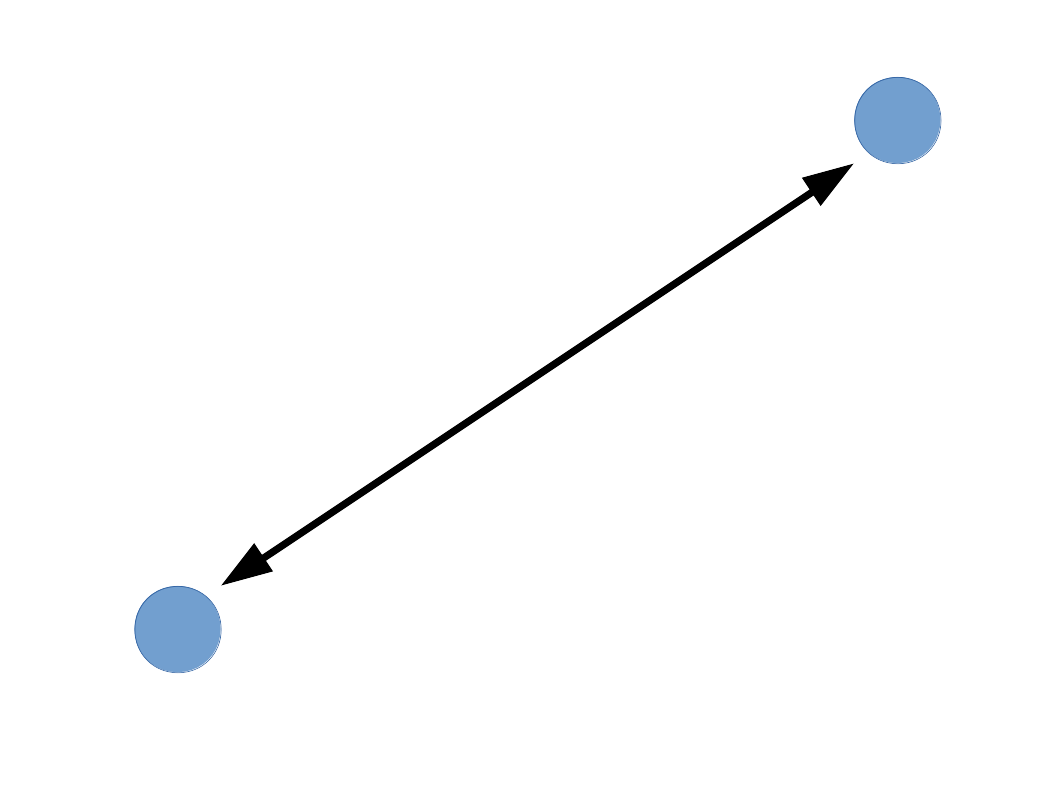
Complejidad algorítmica: N-cuerpos
- 3 partículas: 3 pares posibles $(1,2)$, $(1,3)$, $(2,3)$. (3 "pasos" en el algorítmo)
- ¿$n$ partículas?
- La pregunta es, ¿cuántos pares únicos podemos formar de $n$ partículas?
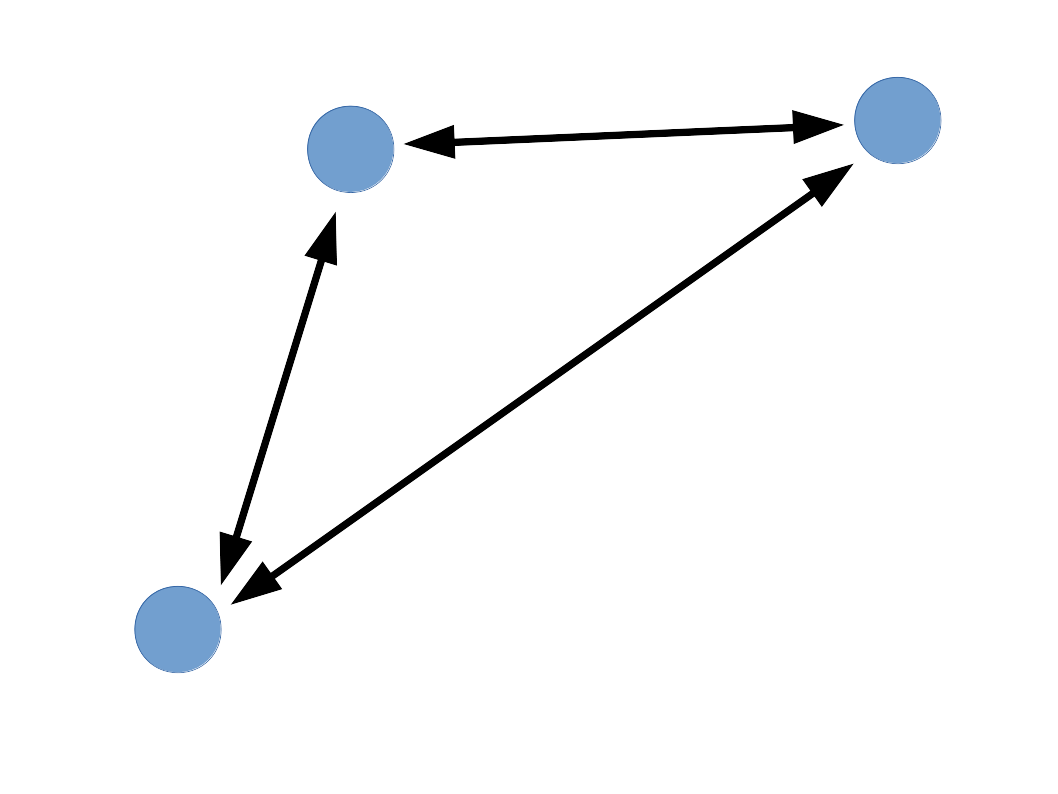
Complejidad algorítmica: N-cuerpos
- Hay $n$ pares para cada partícula (incluyendo un "par" de la partícula con si misma).
- Hay $n$ partículas $\Rightarrow$ número total de pares es $n \times n = n^2$.
- Para eliminar los pares falsos (de una partícula con si misma), de los cuales hay $n$, podemos restar $n$ de $n^2$.
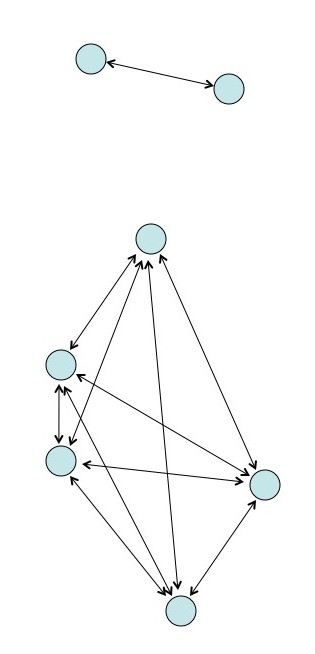
Complejidad algorítmica: N-cuerpos
- Pero, estamos contando los mismos pares dos veces: el par $(3,5)$ es el mismo par como $(5,3)$.
- Multiplicamos por $1/2$, para obtener el número final de pares únicos:
$\frac{1}{2}(n^2 - n)$

Complejidad algorítmica: notación O grande
- La complejidad del algoritmo está dada simplemente por contar el número de pares únicos!
- Expresamos la complejidad en notación "Big-O" (O grande): $\mathcal{O}$.
Complejidad algorítmica: notación O grande
- El número de pares de $n$ partículas es $\frac{1}{2}(n^2 - n)$. Usamos el término del grado más alto del polinomio (sin preocuparnos por los coeficientes).
- Lo anterior se debe a que este término es el que crece más rápido con $n$, y el factor de $1/2$ no es muy importante si $n$ es un número grande.
Complejidad algorítmica: $\mathcal{O}(n^2)$
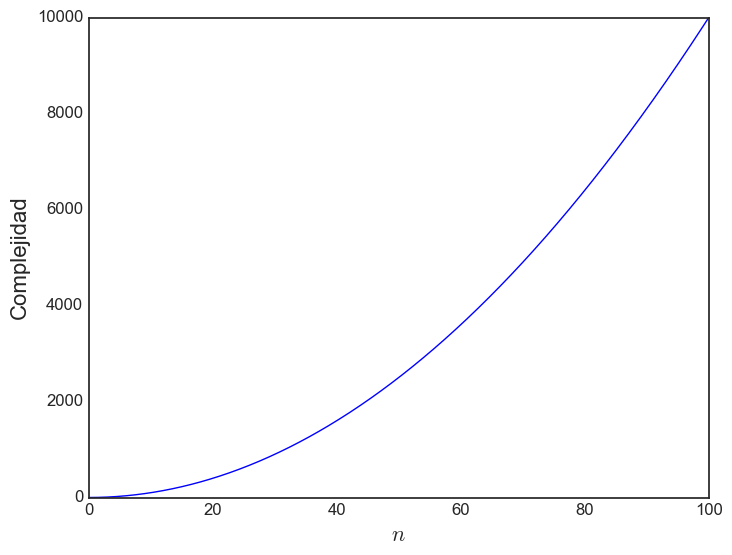
Complejidad algorítmica: notación O grande
- El algoritmo de N-cuerpos tiene una complejidad de $O(n^2)$.
- Si la implementación del algorítmo (i.e. el programa) demora $2$ segundos para $10$ partículas (i.e. $n=10$):
- $t = cn^2$, $2 = c(10^2) \Rightarrow c = 0,02$.
- El programa demorará aproximadamente $200$ segundos para $n = 100$ partículas.
- $t = cn^2$, $t = (0,02) \times (100^2) = 200$.
- Este algoritmo, por lo tanto, escala muy mal: demora mucho más tiempo cuando aumentamos el número de partículas un poco.
Diferentes complejidades
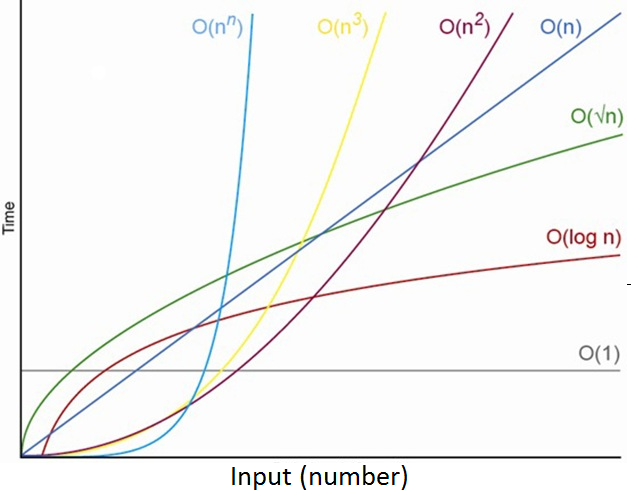
¿Por qué es importante saber la complejidad de un algoritmo?
- Ejemplo: supongamos que tenemos un software para simulaciones de N-cuerpos, pero sin información de su complejidad algorítmica.
- Quizás uno lo usa para simular un cúmulo de estrellas muy pequeño con $20$ partículas, y tarda $1$ hora para completarse.
- Si el algoritmo tiene complejidad $\mathcal{O}(n^2)$ y uno intenta simular una galaxia con 200.000 partículas, se demorará...
11.000 años!
¿En qué momento se deja de esperar?
Precisión
Precisión en la computación
- Estamos todos acostumbrados a calcular cosas en una calculadora (o en el teléfono) y confiar en el resultado.
- Pero, de hecho, los computadores nunca son perfectamente precisos.
- Tienen una memoria finita.
- Utilizan números binarios.
Límites en tamaños de variables
- Almacenar un número en la memoria del computador (en binario) requiere utilizar una cierta cantidad de bits. Pero la memoria no es infinita!
- La mayoría de los lenguajes de programación ponen límites en los tamaños de los números que se puede almacenar en una variable.
- En Python un número normal de tipo float no puede ser mayor que $10^{308}$. ¿Por qué?
Estándar para números de punto flotante
- Existe un estandar en la informática, llamado IEEE754, que define como guardar un número de punto flotante en la memoria de un computador. Se parece a la notación científica.
- En Python hay un total de $64$ bits para guardar un float. De estos:
- $1$ bit es para el signo (+/-)
- $11$ bits son para el exponente
- $52$ bits son para el significando (fracción, mantisa, coeficiente).
Ej: $-5492,0403 \implies -5,4920403\times10^{3}$
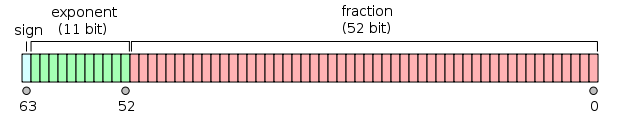
Estándar para números de punto flotante
- Con $11$ bits en el exponente, el rango de números decimales que se puede guardar es de $-1024$ a $1023$.
- $2^{1023}$ es aproximadamente $10^{308} \implies$ número más grande que puede usarse.
Precisión de números de punto flotante
- Entonces, todos los números de punto flotante en un computador están truncados.
- En la mayoría de los lenguajes hay floats de precisión-simple (single-precision) y precisión-doble (double-precision).
- Precisión-doble: $64$ bits. Precisión-simple: $32$ bits:

- Es importante saber cual se ocupa, ya que determina la precisión numérica.
- Ojo: no siempre es más conveniente utilizar Precisión-doble, ya que requiere el doble de memoria que Precisión-simple.
Precisión de la máquina
- El grado de precisión que uno puede obtener en una variable se llama la precisión de la máquina (machine precision), $\epsilon_{M}$.
- No importa el programa que escribamos, ni el algoritmo que usamos, nunca calcularemos valores a una precisión mayor que la precisión de la máquina.
- Las arquitecturas de computadores modernos son de 64-bits.
- Notese que algunos lenguajes permiten control en la cantidad de memoria asignada a variables de distintos tipos, y por eso podemos obtener valores muy pequeños para $\epsilon$ (es decir, precisión extremadamente alta).
En Precisión Doble (64 bits): $\epsilon_{M} = 2^{-53} \approx 1,11 \times 10^{-16}$.
Números que no se puede representar exactamente en binario
- Otro problema: existen números que no podemos representar exactamente en el sistema binario.
- En el sistema decimal, no se puede representar $1/3$ exactamente (es igual a $0.3333333\ldots$).
Números que no se puede representar exactamente en binario
- Por las mismas razones, hay fracciones que no se puede representar exactamente en binario.
- Un ejemplo común es el número $0.1$ (una representación exacta de $1/10$ en el sistema decimal).
- En binario, este tiene la representación $0.000110011001100110011\ldots$.
- Por lo tanto, nunca tendremos el valor $0.1$ representado exactamente en el computador. Siempre habrá un error del tamaño de la precisión de la máquina ($\epsilon_M$).
Resumen
- Algoritmos son procesos estructurados diseñados para resolver un problema específico.
- El primer paso, en cualquier tarea computacional, es pensar sobre el algoritmo, diseñarlo y planificarlo.
- Un programa puede verse como la implementación de un algoritmo.
- Un algoritmo bueno es rápido y preciso.
- La complejidad algorítmica: como escala su tiempo de ejecución con la cantidad de datos que usamos como entrada al algoritmo.
$\Rightarrow$ Notación O-grande (Big-O), $\mathcal{O}$.
Resumen
- La exactitud de los algoritmos está afectada por la precisión de las variables.
- Casi todos los números que se representan en el computador tienen un cierto nivel de imprecisión.
- Debemos estar consciente de esto cuando escribimos programas y hacemos cálculos con el computador.